Является выпуклым многоугольником (или выпуклой многоугольной областью).
Каждое из неравенств в соответствии с теоремой 1 определяет одну из полуплоскостей, являющуюся выпуклым множеством точек (из математики: выпуклое множество точек – если оно вместе с любыми двумя своими точками содержит весь отрезок, соединяющий эти точки). Множеством решений совместной системы линейных неравенств служат точки, которые принадлежат полуплоскостям решений всех неравенств, т.е. их пересечению. Согласно существующей теореме о том, что пересечение (общая часть) любого числа выпуклых множеств есть выпуклое множество – множество решений совместной системы линейных неравенств является выпуклым и содержит конечное число угловых точек, т.е. является выпуклым многоугольником (выпуклой многоугольной областью).
Пример: Построить множество решений системы неравенств
2х1 + 3х2 <= 24 (II) х1 - 3х2 <= 3 (III) x1 >= 0 (IV) 0 <= x2 <= 6 (V, VI)
Координаты угловых точек – вершин многоугольника находятся как координаты точек пересечения соответствующих прямых. Например, точка D – пересечение прямых II и III, т.е. ее координаты являются решением системы
х1 - 3х2 <= 3 (III)
откуда Х1 = 9, Х2 = 2, т.е. D(9;2). Аналогично находятся координаты других угловых точек: О(0;0), А(0;5), В(4/5;6), С(3;6), Е(3;0). При построении областей решений систем неравенств могут встретиться и другие случаи: § множество решений – выпуклая многоугольная область; § одна точка; §
пустое множество, когда систем неравенств несовместима.
Теорему 2 можно обобщить на случай трех и более переменных.
Теорема 3. Множество всех допустимых решений совместной системы m линейных уравнений с n переменными при (m < n) является выпуклым многогранником (или выпуклой многогранной областью в n-мерном пространстве). Доказывать не будем, проиллюстрируем теорему на примере:
х1 + х2 - х4 = 1
С этой целью выразим основные переменные через неосновные:
х4 = -1 + х1 + х2
 Так как рассматриваются допустимые значения переменных, т.е. х1, х2, х3, х4 >= 0, то
-1 + х1 + х2 >=0 (II)
Решением полученной таким образом системы неравенств являются точки четырехугольника ABCD с четырьмя угловыми точками А(0;1), В(0;4), С(6;0), D(1;0). В данном примере графические построения проведены не в пространстве всех переменных, а в плоскости двух неосновных переменных х1 и х2. Но так как любой паре неосновных переменных х1 и х2 соответствуют определенные значения основных переменных х3 и х4, а следовательно одно и только одно решение данной системы уравнений, то каждой точке построенного четырехугольника ABCD соответствует одна и только одна точка множества допустимых решений системы, представляющего в данном случае выпуклый многогранник в четырехмерном пространстве. Утверждение. Между допустимыми базисными решениями и угловыми точками множества допустимых решений системы линейных уравнений существует взаимооднозначное соответствие. Не будем доказывать, опять ограничимся примером. Для системы, приведенной выше можно получить четыре допустимых базисных решения. Группы основных переменных могут быть любые, т.к. все определители не равны 0: х1 и х2 (х3, х4 = 0) – недопустимое (т.к. х1 = -9, х2 = 10), х1 и х3 (х2, х4 = 0) – допустимое Х1 = (1;0;10;0), х1 и х4 (х2, х3 = 0) – допустимое Х2 = (6;0;0;5), х2 и х3 (х1, х4 = 0) – допустимое Х3 = (0;1;9;0), х2 и х4 (х1, х3 = 0) – допустимое Х4 = (0;4;0;3), х3 и х4 (х1, х2 = 0) – недопустимое (т.к. х3 = 12, х4 = -1). Из рисунка, иллюстрирующего решение, видно, что этим допустимым базисным решениям соответствуют угловые точки D(1;0), С(6;0), А(0;1) и В(0;4) четырехугольника ABCD.
|
-5х1 + 4х2 <= 20 (I)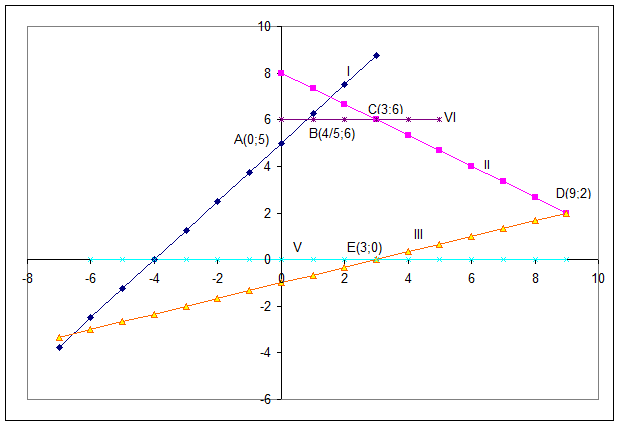
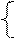2х1 +3х2 <= 24 (II)
= 1 *(- 1) – 0 * 0 = -1), и неосновные (свободные) переменные х1 и х2, и вместо множества решений системы уравнений построить множество значений их неосновных переменных (это выполнить возможно, т.к. неосновных переменных всего две).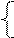
х3 = 12 – 2х1 – 3х2
