Описание установки и метода измерений. Маховик состоит из диска 1 и шкива 2, насаженных на вал (рис
При падении груза маховик начинает вращаться с угловым ускорением b. Результирующий момент, создающий это ускорение, складывается из момента М н силы натяжения нити и момента М тр силы трения в подшипниках вала. Так как направления этих моментов противоположны, то уравнение (1) можно представить в виде
Если момент инерции маховика и момент силы трения остаются постоянными, то зависимость углового ускорения от момента силы натяжения линейная и графически изображается прямой линией (рис 2).
где r и D - радиус и диаметр шкива. Так как груз движется из состояния покоя равноускоренно, то
где h – путь, пройденный грузом за время t. Подставив выражение (4) в уравнение (3), получим формулу, по которой можно рассчитать на опыте угловое ускорение маховика
Модуль момента силы натяжения числено равен произведению силы натяжения F н на плечо силы, которое является радиусом шкива:
Силу натяжения нити найдем, рассматривая движение груза3. На него действуют сила тяжести P и сила реакции нити F 1. По второму закону Ньютона Учитывая, что сила натяжения нити, действующая на шкив и сила реакции, действующая на груз, одинаковы по величине (F н = F 1), получим
Тогда
Подставив в уравнение (6) выражение (4) для ускорения a, получим формулу
по которой можно рассчитать на опыте момент силы натяжения нити, действующей на маховик.
|

 Маховик состоит из диска 1 и шкива 2, насаженных на вал (рис. 1). Вал может вращаться около горизонтальной оси OO'. На шкив намотана нить, к свободному концу которой подвешен груз 3.
Маховик состоит из диска 1 и шкива 2, насаженных на вал (рис. 1). Вал может вращаться около горизонтальной оси OO'. На шкив намотана нить, к свободному концу которой подвешен груз 3.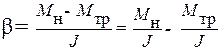 . (2)
. (2) Из уравнения (2) следует, что при покоящемся маховике (b=0) М н = М тр. Только когда момент силы натяжения становится больше максимального момента силы трения покоя, маховик начинает вращаться равноускоренно. Прямая на графике пересекает ось абсцисс (рис. 2) в точке, которая определяет М тр. Угловое ускорение маховика b можно найти, зная тангенциальное ускорение a t точек боковой поверхности шкива, которое равно ускорению a падающего груза:
Из уравнения (2) следует, что при покоящемся маховике (b=0) М н = М тр. Только когда момент силы натяжения становится больше максимального момента силы трения покоя, маховик начинает вращаться равноускоренно. Прямая на графике пересекает ось абсцисс (рис. 2) в точке, которая определяет М тр. Угловое ускорение маховика b можно найти, зная тангенциальное ускорение a t точек боковой поверхности шкива, которое равно ускорению a падающего груза: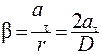 , (3)
, (3)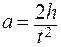 , (4)
, (4) . (5)
. (5) .
. , где m - масса подвешенного к нити груза.
, где m - масса подвешенного к нити груза. .
. . (6)
. (6) , (7)
, (7)


