Описание установки и метода измерений. Маятник Обербека (рис. 1) представляет собой маховик, которому придана крестообразная форма
Рассмотрим силы, действующие на груз. На груз действуют две силы: сила тяжести P = mg и сила натяжения нити F н. Спроецируем эти силы на ось X, которую направим вертикально вниз. Напишем второй закон Ньютона для поступательного движения груза
ma = mg – F н. (1)
Так как масса нити пренебрежимо мала, то согласно третьему закону Ньютона, сила натяжения нити F н', действующая на маховик, равна силе натяжения (реакции) нити F н, действующей на груз:
| F н'| = | F н|. (2)
На маятник Обербека действуют момент силы натяжения M н' нити и момент силы трения M тр в подшипниках. Основной закон динамики вращательного движения относительно оси, перпендикулярной плоскости рисунка, выразится уравнением
M н' – M тр = J β, (3)
где J – момент инерции маятника Обербека, β – его угловое ускорение. Так как в нашем опыте M тр<< M н', то уравнение (3) можно заменить уравнением M н = J β. (4)
Момент силы натяжения равен произведению силы натяжения F н' на плечо силы, являющееся радиусом шкива r:
M н' = F н'· r = F н'· D /2, (5)
где D – диаметр шкива. Из уравнения (1) F н = m (g – a). (6)
С учетом (2) и (6) формула (5) примет вид
Груз движется вниз равноускоренно, поэтому пройденный путь h определяется уравнением кинематики
из которого выражаем линейное ускорение
Расчет ускорения по формуле (9) показывает, что в условиях нашего опыта a << g, поэтому уравнение (7) упрощаем до вида
Угловое ускорение β связано с линейным (тангенциальным) ускорением точек боковой поверхности шкива, равным ускорению груза m, соотношением
Тогда, учитывая (9), получим
Из уравнения (4) следует, что при J = const в случае действия на маховик двух различных моментов сил M 1 и M 2 отношение этих моментов прямо пропорционально отношению угловых ускорений
Согласно уравнениям (10) и (11) при D = const и h = const
Для проверки равенства (12) необходимо по результатам опыта определить отношение моментов сил по формуле (13) и отношение угловых ускорений по формуле (14) и сравнить эти отношения. Для определения отношений (13) и (14) нужно изменять вращающий момент, подвешивая к нити грузы разной массы m 1 и m 2, не изменяя положения грузов m 0 на стержнях. Согласно (4), угловое ускорение β обратно пропорционально J при M = const. Если построить график зависимости 1/β = f (J) при M = const, то его линейность должна подтвердить обратно пропорциональную зависимость β от J. Величину, обратную β, найдем из (11):
Момент инерции маятника Обербека может быть определен как сумма моментов инерции крестовины со шкивом и грузов m 0. Если размеры грузов малы по сравнению с расстоянием R от центра груза до оси вращения, то их моменты инерции можно определить как моменты инерции материальных точек. Таким образом, J = J 0 + km 0 R 2, (16)
где J 0 – момент инерции крестовины со шкивом, m 0 – масса груза, k – количество грузов. Из формулы (16) следует, что момент инерции маятника Обербека можно изменить, меняя количество грузов на крестовине и их расстояние до оси вращения.
|

 Маятник Обербека (рис. 1) представляет собой маховик, которому придана крестообразная форма. На четырех стержнях насажены грузы одинаковой массы m 0, которые могут быть закреплены на различных расстояниях R от оси вращения. На общей оси с маховиком насажены два шкива. На тот или иной шкив намотана нить, к свободному концу её, переброшенному через блок, прикреплен груз массой m. Под действием груза нить разматывается без скольжения и приводит маховик в равноускоренное вращательное движение.
Маятник Обербека (рис. 1) представляет собой маховик, которому придана крестообразная форма. На четырех стержнях насажены грузы одинаковой массы m 0, которые могут быть закреплены на различных расстояниях R от оси вращения. На общей оси с маховиком насажены два шкива. На тот или иной шкив намотана нить, к свободному концу её, переброшенному через блок, прикреплен груз массой m. Под действием груза нить разматывается без скольжения и приводит маховик в равноускоренное вращательное движение.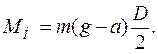 (7)
(7)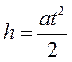 , (8)
, (8)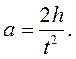 (9)
(9)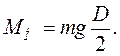 (10)
(10)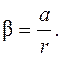
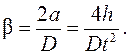 (11)
(11)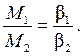 (12)
(12) (13)
(13)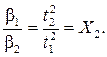 (14)
(14)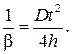 (15)
(15)


