Описание установки и метода измерения
Большинство косвенных методов измерения ускорения свободного падения g основано на использовании формулы для периода гармонических колебаний физического маятника
В данной работе это достигается путем использования физического маятника в форме длинного стержня. Маятник представляет собой однородный стержень (рис. 1) с опорной призмой П, которую можно перемещать вдоль стержня и закреплять в любом его месте. Для определения положения призмы на стержне нанесена шкала с делениями через 1 см. Период колебаний маятника, который выражается формулой (1), можно записать в виде
где Момент инерции стержня относительно оси качания запишем по теореме Штейнера:
где J 0 момент инерции стержня относительно оси, проходящей через центр массы C (середину стержня) параллельно оси качания. Для стержня
Для любого тела момент инерции J 0 можно представить в виде
Величина a 0 называется радиусом инерции и имеет определенное значение для каждого тела. Для стержня
Используя формулы (3) и (4), получим выражение для приведенной длины
и периода колебаний
Таким образом, приведенная длина и, следовательно, период колебаний маятника являются функциями расстояния от центра массы до оси качания. Из этих формул видно, что L и T стремятся к бесконечности при двух значениях a: при a ®0 и при a ®¥. Для определения значений при которых период является экстремальным, найдем производную d L /d a и приравняем ее к нулю:
Из графика (риc. 2) видно, что при увеличении или уменьшении расстояния a по сравнению с a 0 период колебания увеличивается. Поэтому одно и то же значение периода, большее чем T min, маятник может иметь при двух положениях опорной призмы: при
откуда
Приведенная длина (рис. 2) L = MN + MK. Очевидно, что другому периоду колебаний будет соответствовать другая приведенная длина. После подстановки (5) в (2) получим
откуда
Формула (6) является расчетной для вычисления ускорения свободного падения. Значения
|

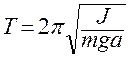 , (1)
, (1) где J - момент инерции маятника относительно оси качания (точки подвеса), m - масса маятника, a - расстояние от центра массы до оси качания (см. рис. 1). Однако формула (1) непосредственно для вычисления g не используется, так как момент инерции J и расстояние a
где J - момент инерции маятника относительно оси качания (точки подвеса), m - масса маятника, a - расстояние от центра массы до оси качания (см. рис. 1). Однако формула (1) непосредственно для вычисления g не используется, так как момент инерции J и расстояние a  обычно не могут быть измерены достаточно точно. Поэтому применяются такие методы, которые позволяют исключить данные величины из расчетной формулы для вычисления g.
обычно не могут быть измерены достаточно точно. Поэтому применяются такие методы, которые позволяют исключить данные величины из расчетной формулы для вычисления g.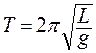 , (2)
, (2)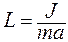 называется приведенной длиной физического маятника.
называется приведенной длиной физического маятника.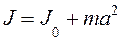 , (3)
, (3)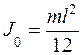 .
.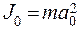 . (4)
. (4)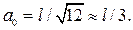
 ,
,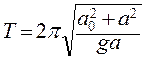 .
. ,
, откуда a = ± a 0.Значит, T = T min, если опорная призма закреплена на расстоянии a 0» l/3 от середины стержня. Второе расстояние a = a 0 означает, что если перевернуть стержень, то для точек подвеса, симметричных относительно середины, периоды колебаний будут одинаковы.
откуда a = ± a 0.Значит, T = T min, если опорная призма закреплена на расстоянии a 0» l/3 от середины стержня. Второе расстояние a = a 0 означает, что если перевернуть стержень, то для точек подвеса, симметричных относительно середины, периоды колебаний будут одинаковы.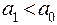 и
и 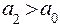 . Для этих положений опорной призмы будут одинаковы и приведенные длины маятника, что следует, из формулы (2):
. Для этих положений опорной призмы будут одинаковы и приведенные длины маятника, что следует, из формулы (2):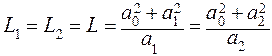 ,
,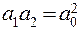 . Тогда
. Тогда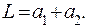 (5)
(5)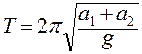 ,
, . (6)
. (6)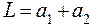 и T определяют по экспериментально построенному графику. Для этого опорную призму перемещают вдоль стержня и для каждого ее положения измеряют период колебаний. При проведении опыта и построении графика вместо расстояния a удобнее брать расстояние от конца стержня до призмы, которое на рис. 1 обозначено х.
и T определяют по экспериментально построенному графику. Для этого опорную призму перемещают вдоль стержня и для каждого ее положения измеряют период колебаний. При проведении опыта и построении графика вместо расстояния a удобнее брать расстояние от конца стержня до призмы, которое на рис. 1 обозначено х.


