Продифференцировав дважды функцию (2) по времени, получим
а = - w 2 A cos (w t + a) = - w 2x. (4)
После подстановки (4) в (3) находим
w =
Последняя формула выражает период собственных колебаний пружинного маятника, который зависит только от свойств колеблющейся системы: от массы груза и коэффициента упругости пружины. В данной работе делается проверка справедливости закона Гука и определяется коэффициент упругости пружины. При этом определение коэффициента упругости k делается двумя способами: из закона Гука (статический способ) и из измерений периода колебаний маятника (динамический способ). Совпадение значений k, найденных различными способами, будет указывать на правильность теории пружинного маятника.
|
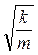и Т = 2p 
. (5)
