Примеры использования алгебраического аппарата для классических экономических моделей.
Модель Леонтьева многоотраслевой экономики Макроэкономика функционирования межотраслевого хозяйства требует баланса между отдельными отраслями. Каждая отрасль, с одной стороны, является производителем, а с другой – потребителем продукции, выпускаемой другими отраслями. Возникает задача расчета связи между отраслями через выпуск и потребление продукции разного вида. Впервые эта проблема была сформулирована в виде математической модели в 1936 г. американским экономистом В.В. Леонтьевым. Модель основана на алгебре матриц и использует аппарат матричного анализа. Предполагается, что производственная сфера хозяйства представляет собой
Балансовый принцип связи различных отраслей состоит в том, что валовой выпуск
В основу модели Леонтьева лег установленный им факт, что в течении длительного времени уровень технологии производства остается неизменным, откуда следует, что
Систему (1.9) можно записать в матричном виде, называемом уравнением линейного межотраслевого баланса:
где Уравнение (1.10) можно использовать в двух целях: для вычисления неизвестного вектора валового выпуска Матрица Требование неотрицательности элементов матрицы Известно, что если для матрицы Таким образом, для определения продуктивности матрицы Перепишем систему (1.10) с использованием единичной матрицы
Если существует обратная матрица
Матрица Теорема (первый критерий продуктивности). Матрица Теорема (второй критерий продуктивности). Матрица
причем хотя бы для одного столбца (строки) неравенство строгое. Пример 15. Дана матрица коэффициентов прямых затрат, вектор валового выпуска для трех отраслей промышленности за истекший год и планируемый на следующий год вектор конечного потребления. Найти вектор конечного потребления за истекший период. Определить объем валового выпуска каждого вида продукции на следующий год.
Решение. Выпишем вектор валового выпуска и матрицу коэффициентов прямых затрат:
Очевидно, что матрица Для определения вектора конечного потребления за истекший период используем уравнение (1.11). Имеем:
Находим вектор конечного продукта за истекший период:
Для ответа на второй вопрос – определение объема валового выпуска каждого вида продукции на следующий год, используем формулу (1.12). Сначала вычислим матрицу прямых затрат:
Таким образом, чтобы выполнить план по выпуску конечного продукта, нужно увеличить соответствующие валовые выпуски: добычу и переработку углеводородов на 52,1%, уровень энергетики – на 35,8% и выпуск продукции машиностроения – на 85% по сравнению с прошедшим годом. n
Линейная модель торговли
Рассмотрим линейную модель обмена или модель международной торговли, отражающую процесс взаимных закупок товаров. Будем полагать, что бюджеты
Матрица Для
Условие сбалансированной (бездефицитной) торговли: для каждой страны ее бюджет не должен превышать выручки от торговли, т.е.
В условиях нашей модели неравенства обращаются в равенства. Действительно, если сложить все эти неравенства и сгруппировать по
Таким образом, условия (1.15) принимают вид системы линейных уравнений:
Если ввести вектор бюджетов
Это уравнение означает, что собственный вектор структурной матрицы Для определения
Пример 16. Структурная матрица торговли четырех стран имеет вид:
Найти бюджеты этих стран, удовлетворяющие сбалансированной бездефицитной торговле при условии, что сумма бюджетов равна 6270 д.е. Решение. Из уравнения (1.18) имеем систему:
Ранг матрицы этой системы равен трем, значит, одна из неизвестных является свободной, а остальные выражаются через нее. Решить эту систему можно методом Гаусса (проделайте самостоятельно!). Найденные компоненты собственного вектора
Приравниваем сумму найденных значений к заданной сумме бюджетов:
Окончательно получаем искомые величины бюджетов стран при бездефицитной торговле (в д.е.):
|

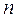 отраслей, каждая из которых производит свой однородный продукт. Для обеспечения своего производства каждая отрасль нуждается в продукции других отраслей (производственное потребление). Как правило, рассматривается процесс производства за один год. Обозначим
отраслей, каждая из которых производит свой однородный продукт. Для обеспечения своего производства каждая отрасль нуждается в продукции других отраслей (производственное потребление). Как правило, рассматривается процесс производства за один год. Обозначим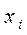 - общий объем продукции
- общий объем продукции 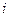 -й отрасли (ее валовой выпуск);
-й отрасли (ее валовой выпуск);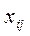 - объем продукции
- объем продукции  -й отраслью при производстве объема продукции
-й отраслью при производстве объема продукции 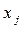 ;
;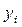 - объем продукции
- объем продукции 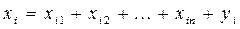 ,
, 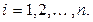 (1.8)
(1.8) - объем потребления
- объем потребления 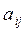 называются коэффициентами прямых затрат. Таким образом, учитывая что
называются коэффициентами прямых затрат. Таким образом, учитывая что 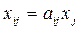 для
для 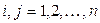 , уравнения (1.8) имеют вид:
, уравнения (1.8) имеют вид: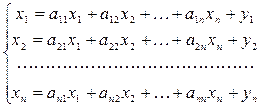 (1.9)
(1.9)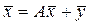 , (1.10)
, (1.10) - вектор валового выпуска,
- вектор валового выпуска, 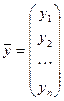 - вектор конечного потребления,
- вектор конечного потребления, 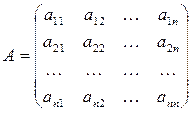 - матрица коэффициентов прямых затрат.
- матрица коэффициентов прямых затрат.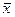 или для нахождения вектора конечного потребления
или для нахождения вектора конечного потребления 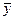 .
.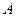 , все элементы которой неотрицательны, называется продуктивной, если для любого вектора
, все элементы которой неотрицательны, называется продуктивной, если для любого вектора 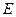 :
: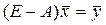 . (1.11)
. (1.11) , существует единственное решение уравнения (1.11):
, существует единственное решение уравнения (1.11):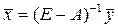 . (1.12)
. (1.12) ,
,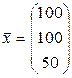 ,
, 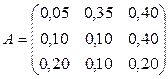
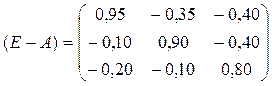 .
.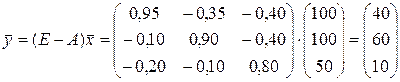 .
.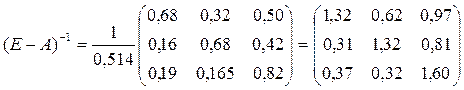 .
.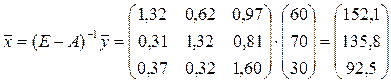 .
. стран, которые мы обозначим соответственно
стран, которые мы обозначим соответственно 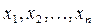 , расходуются на покупку товаров. Пусть
, расходуются на покупку товаров. Пусть 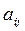 - доля бюджета
- доля бюджета 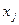 , которую
, которую 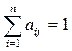 . (1.13)
. (1.13)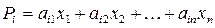 ,
, 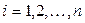 . (1.14)
. (1.14)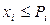 , или
, или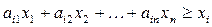 ,
,  . (1.15)
. (1.15)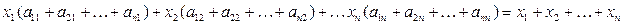 .
.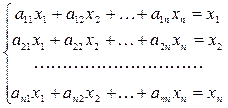 . (1.16)
. (1.16)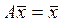 . (1.17)
. (1.17)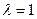 , состоит из бюджетов стран бездефицитной международной торговли.
, состоит из бюджетов стран бездефицитной международной торговли.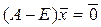 . (1.18)
. (1.18)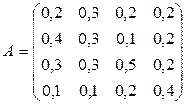 .
.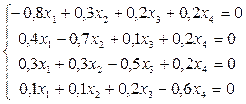 .
.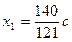 ,
, 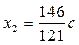 ,
, 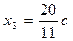 ,
, 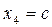 .
.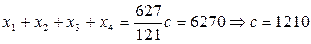 .
.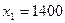 ,
, 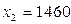 ,
, 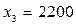 ,
, 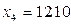 . n
. n


