Свойства ранга матрицы
1) Ранг матрицы 2) 3) Если
Нахождение ранга матрицы, используя непосредственно определение, довольно громоздко и трудоемко.
Теорема 4. Ранг матрицы не изменяется при ее элементарных преобразованиях.
С помощью элементарных преобразований можно привести матрицу к верхнетреугольному виду:
где
Пример 12. Найти ранг матрицы
Решение. Используя технику элементарных преобразований (как в методе Гаусса), получим верхнетреугольную матрицу:
Таким образом,
Понятие ранга матрицы тесно связано с понятием линейной зависимости (независимости) ее строк (столбцов). Строка (столбец) называются линейно зависимыми, если хотя бы одна из строк (столбцов) линейно выражается через остальные. В противном случае, строки (столбцы) называются линейно независимыми (подробнее читайте в п. 1.6.1).
Теорема 5. Ранг матрицы равен максимальному числу ее линейно независимых строк (столбцов).
|
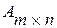не превосходит меньшего из ее размеров, т.е.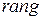 
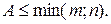
тогда и только тогда, когда 
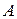– нулевая матрица.
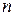-го порядка, то 
тогда и только тогда, когда матрица 
,
, 
; 
. Ранг верхнетреугольной матрицы равен 
.
.
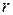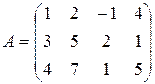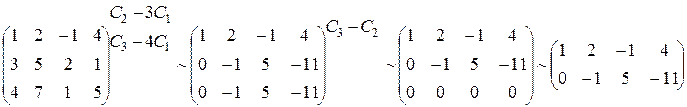
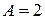.n
