Метод Гаусса. Как было отмечено выше, метод Крамера и матричный метод имеют один существенный недостаток: они неприменимы
Как было отмечено выше, метод Крамера и матричный метод имеют один существенный недостаток: они неприменимы, если определитель системы равен нулю. В связи с этим, рассмотрим еще один, наиболее универсальный метод решения систем линейных алгебраических уравнений – метод Гаусса.
Пусть число уравнений системы совпадает с числом неизвестных1.
Расширенной матрицей системы (1.2) называется матрица системы, дополненная столбцом свободных членов:
Расширенная матрица системы называется верхнетреугольной, если в матрице системы все элементы ниже главной диагонали равны нулю:
Расширенную матрицу системы мы будем называть диагональной, если матрица системы представляет собой единичную:
К элементарным преобразованиям расширенной матрицы системы относятся преобразования трех типов:
1) Перемена местами любых двух строк:
2) Умножение любой строки на любое число, отличное от нуля
3) Прибавление к любой строке любой другой, умноженной на произвольное число:
Известно, что элементарные преобразования расширенной матрицы системы приводят к эквивалентной матрице, т.е. система линейных алгебраических уравнений, соответствующая полученной матрице, имеет те же решения, что и исходная. Идея метода Гаусса заключается в том, чтобы с помощью элементарных преобразований от расширенной матрицы системы вида (1.3) перейти вначале к верхнетреугольной матрице (1.4) (прямой ход метода Гаусса), а затем и к диагональной (1.5) (обратный ход метода Гаусса). Если при переходе к верхнетреугольной матрице в матрице системы не возникло ни одной нулевой строки (это соответствует тому, что определитель исходной системы отличен от нуля), то система имеет единственное решение. Его легко найти, исходя из диагонального вида:
Продемонстрируем на примерах технику использования элементарных преобразований.
Пример 8. Решить систему уравнений Решение. Запишем расширенную матрицу системы:
Выберем в первом столбце ведущий элемент, т.е. элемент, с помощью которого удобно будет сделать нули под ним. Таким числом является единица. Поменяем местами первую и третью строки (
С помощью элементарных преобразований 3-го типа делаем нули под ведущим элементом (
Теперь выбираем ведущий элемент во втором столбце. Поскольку пока единицы нет, то её желательно создать. Для этого из второй строки вычтем удвоенную третью (
Делаем нуль под ведущим элементом (
Умножим третью строку на
Мы получили матрицу верхнетреугольного вида. Переходим к обратному ходу метода Гаусса. В качестве ведущего элемента выбираем единицу, стоящую в третьем столбце. Делаем нули над ней (
Последний шаг. С помощью единицы во втором столбце зануляем элемент над ней (
Получена матрица диагонального вида. Проверку полученного решения сделайте самостоятельно. Ответ: Если при переходе к верхнетреугольной матрице в матрице системы возникает хотя бы одна нулевая строка (это означает, что
Пример 9. Решить систему уравнений
Решение.
Распишем последнюю строку полученной матрицы в виде уравнения:
Очевидно, что это уравнение, а значит и вся система, решений не имеет. n
Пример 10. Решить систему уравнений Решение.
Таким образом, Это общее решение системы. Присваивая свободной переменной
Ответ: Отметим ещё одно достоинство метода Гаусса. Для систем линейных уравнений 4-го порядка и выше метод Гаусса оказывается эффективнее метода Крамера и матричного метода и приводит к решению гораздо быстрее.
Пример 11. Решить систему уравнений
Решение.
Проверку сделайте самостоятельно. Ответ:
|




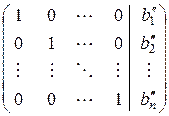
 .
.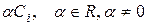 .
. .
. .
. .
.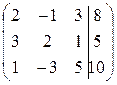 .
.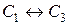 элементарное преобразование 1-го вида):
элементарное преобразование 1-го вида):

 ):
): .
.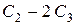 ):
):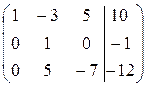 .
. ):
):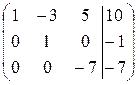 .
.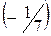 (
( – элементарное преобразование 2-го типа):
– элементарное преобразование 2-го типа):
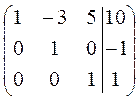 .
. ):
):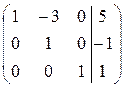 .
.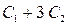 ):
):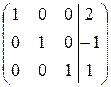 .
. .n
.n




 .
.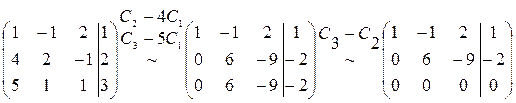 .
.
 В отличие от предыдущего примера, последняя строка непротиворечива. Она указывает на то, что третье уравнение системы является следствием первых двух. Таким образом, мы, фактически, получили систему из двух уравнений с тремя неизвестными. Такая система имеет бесчисленное множество решений. Для того чтобы их найти, одну из переменных (её называют свободной) переносят в правую часть расширенной матрицы, а остальные переменные (их называют базисными или связными) выражают через эту свободную. Имеем
В отличие от предыдущего примера, последняя строка непротиворечива. Она указывает на то, что третье уравнение системы является следствием первых двух. Таким образом, мы, фактически, получили систему из двух уравнений с тремя неизвестными. Такая система имеет бесчисленное множество решений. Для того чтобы их найти, одну из переменных (её называют свободной) переносят в правую часть расширенной матрицы, а остальные переменные (их называют базисными или связными) выражают через эту свободную. Имеем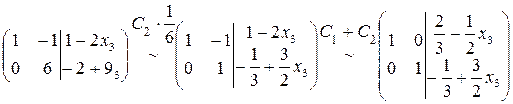 .
.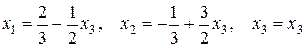 .
.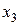 конкретные значения, можно получать частные решения, например,
конкретные значения, можно получать частные решения, например,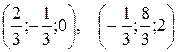 и т.д.
и т.д. .n
.n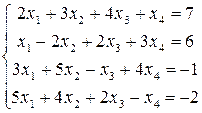 .
.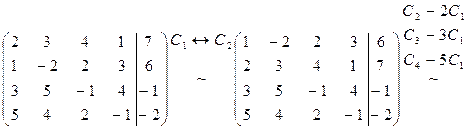


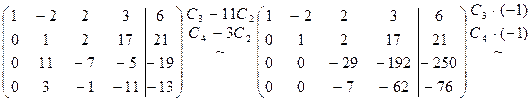



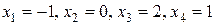 .n
.n


