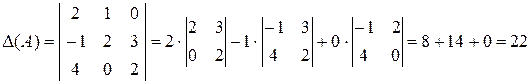Свойства определителей
1. Определитель не меняется при транспонировании. 2. Если все элементы какой-либо строки (или столбца) равны нулю, то определитель равен 0. 3. Если две строки (два столбца) поменять местами, то определитель меняет знак. 4. Если элементы какой-либо строки (столбца) содержат общий множитель, то его можно вынести за знак определителя. 5. Если в определителе две строки (два столбца) одинаковы или пропорциональны, то определитель равен 0. 6. Справедливо равенство
7. Определитель не изменится, если к элементам какой-либо его строки (столбца) прибавить элементы другой строки (столбца), умноженные на одно и то же число. 8. Сумма произведений элементов любой строки (столбца) на свои алгебраические дополнения равна самому определителю. 9. Сумма произведений элементов любой строки (столбца) определителя на алгебраические дополнения другой строки (столбца) равна 0.
Теорема 1. Если
Следствие.
Пример 5. (Образец решения задачи 2 из контрольной работы). Даны матрицы Решение.
Таким образом,
|
.
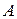и 
– квадратные матрицы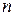 
-го порядка, то
.
.
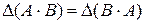и 
. Проверить справедливость равенства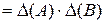 
.
