Матричный метод. Обозначим через матрицу системы (1.1), т.е
Обозначим через
через Принимая во внимание правило умножения матриц, можно систему линейных уравнений (1.1) записать в виде матричного уравнения:
решение которого имеет вид
Пример 7. (Образец выполнения задачи 1 из контрольной работы) Решить систему уравнений двумя способами:
Решение. Используем метод Крамера:
Тогда
Проверим правильность полученных решений, для чего подставим их в условие:
Теперь решим ту же систему матричным методом. Найдем обратную матрицу
Определитель матрицы найден выше (фактически это Следовательно,
Ответ: Замечание 1. Метод Крамера и матричный метод применимы для систем любого конечного порядка при двух условиях: количество уравнений совпадает с количеством неизвестных и определитель системы отличен от нуля. Замечание 2. Если определитель системы равен нулю, то система либо не имеет решений вообще, либо имеет бесконечное множество решений.
|
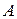матрицу системы (1.1), т.е. матрицу, составленную из коэффициентов при неизвестных:
,
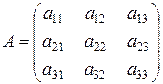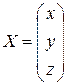– матрицу-столбец из неизвестных и через 
– матрицу-столбец правых частей.
,
.
.
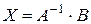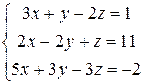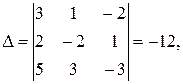
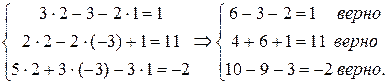
к матрице системы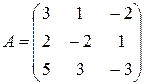 
. Вычислим все алгебраические дополнения:
; 
; 
;
; 
; 
;
; 
; 
.
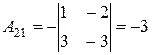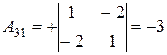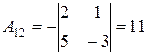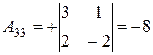) и равен -12.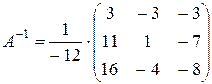
. Тогда
.
.n
