Определители. Понятие определителя вводится только для квадратных матриц
Понятие определителя вводится только для квадратных матриц. Рассмотрим квадратную матрицу 2 го порядка: Определителем 2 го порядка матрицы
Пример 3. Вычислить определитель матрицы Решение.
Пусть Минором элемента Алгебраическим дополнением элемента
Определителем 3 го порядка (матрицы
Пример 3. Вычислить определитель матрицы Решение. Находим миноры и алгебраические дополнения элементов 1-ой строки матрицы:
Вычисляем исходный определитель
В дальнейшем при вычислении определителей мы будем пользоваться более короткой записью:
Далее индуктивно вводится понятие определителей более высоких порядков.
Определителем
|
.
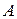называется число:
.
.
n
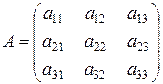– матрица 3 го порядка.
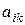называется определитель 
, составленный из элементов, оставшихся после вычеркивания из матрицы 
-той строки и 
-того столбца.
.
.
.
;
;
.
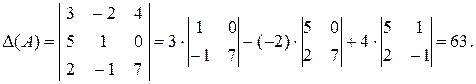n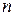
-го порядка называется сумма произведений элементов 1-ой строки на их алгебраические дополнения.
