Собственные векторы и собственные значения матрицы
Вектор
Число
Равенство (1.6) можно записать в развернутом виде:
Откуда получим
или в матричном виде
Полученная система всегда имеет нулевое решение. Для существования ненулевого решения необходимо и достаточно, чтобы определитель системы обращался в нуль:
Определитель
Теорема 6. Корни характеристического уравнения матрицы
Пример 13. Найти собственные значения и собственные векторы матрицы:
Решение. Составим характеристическое уравнение
откуда собственные значения матрицы Находим собственный вектор
откуда
Пример 14. Найти собственные значения и собственные векторы матрицы:
Решение. После преобразований (проделайте это самостоятельно) характеристическое уравнение примет вид:
Имеем далее
откуда Найдем собственный вектор
Решая полученную систему методом Гаусса, получим Аналогично находим, что
|

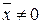 называется собственным вектором матрицы
называется собственным вектором матрицы  , если найдется такое число
, если найдется такое число  , что
, что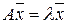
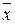 .
. .
.
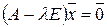 .
.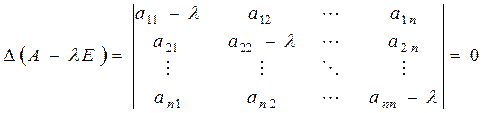
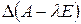 является многочленом
является многочленом  -ой степени. Он называется характеристическим многочленом матрицы
-ой степени. Он называется характеристическим многочленом матрицы  .
.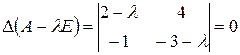 или
или  ,
, ,
,  .
. , соответствующий собственному значению
, соответствующий собственному значению  . Для этого решаем матричное уравнение:
. Для этого решаем матричное уравнение: или
или  ,
, , т.е.
, т.е. 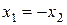 . Положив
. Положив  , мы получим, что вектор
, мы получим, что вектор 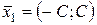 при любом
при любом 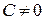 является собственным вектором матрицы
является собственным вектором матрицы 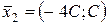 при любом
при любом 
 .
.
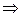
 ,
, ,
,  .
.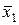 , соответствующий собственному значению
, соответствующий собственному значению 
 , где
, где 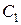 и
и 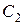 произвольные числа не равные нулю одновременно.
произвольные числа не равные нулю одновременно. при любом
при любом 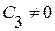 есть собственный вектор матрицы
есть собственный вектор матрицы 


