Равновесие при экстракции
Равновесие для систем жидкость – распределяемое вещество – жидкость следует закону распределения. Согласно этому закону, отношение равновесных концентраций распределяемого компонента между двумя фазами, и жидкими в том числе, при постоянной температуре есть величина постоянная. Эта величина, как уже было сказано выше, представляет собой коэффициент распределения:
При представлении состава фаз в относительных массовых концентрациях уравнение равновесия имеет вид
При малых концентрациях
Если пренебречь взаимной растворимостью жидкостей, составляющих фазы На практике коэффициент равновесия не является величиной постоянной: он зависит не только от природы взаимодействующих веществ, температуры и давления, но и от концентрации. Поэтому линия равновесия в системе координат
|
.
.
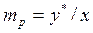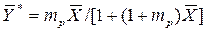в растворе произведением 
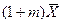пренебрегают и уравнение равновесие приобретает вид
.
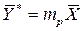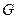и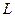 
, то каждая из фаз будет представлять двухкомпонентный раствор. Линия равновесия в системе координат 
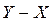будет прямой.
является кривой и строится по справочным данным, полученным из опыта. При частичной взаимной растворимости жидкостей каждая из жидких фаз представляет собой трехкомпонентный раствор, состав которого невозможно отложить на диаграмме в координатах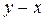 
. Составы таких трехкомпонентных фаз удобно представлять в треугольной системе координат (треугольной диаграмме). Правила применения треугольных диаграмм для анализа процессов экстракции приведены в технической литературе. Однако при проектировании и расчете экстракционных аппаратов в виду их сложности приходится использовать допущение о взаимной нерастворимости распределяющих фаз.
