Материальный баланс экстракции
Примем следующие обозначения: исходная смесь
Интегрируя уравнение в пределах от начальных до текущих значений концентраций
В случае частичной взаимной растворимости фаз Уравнение материального баланса по общим потокам имеет вид
по распределяемому компоненту
где
Кинетические закономерности процесса экстракции
Кинетические закономерности процесса экстракции определяются основными законами массопередачи. При экстракции имеет место массообмен между двумя жидкими фазами, распределяемое вещество в этом процессе переходит из одной жидкости в другую. Для развития поверхности фазового контакта одну из жидкостей диспергируют в другой. Распределяемое вещество переходит из сплошной фазы к поверхности капли и затем внутрь ее или из капли через поверхность раздела фаз в ядро потока сплошной фазы. Если диффузионное сопротивление процессу массопередаче сосредоточено внутри капли, то коэффициент массопередачи может быть принят равным коэффициенту массоотдачи дисперсной фазы для капель малого и среднего диаметра (
для
где Если диффузионное сопротивление внутри капли незначительно по сравнению с диффузионным сопротивлением в сплошной фазе (
или
где Если диффузионным сопротивлением сплошной и дисперсной фаз пренебречь нельзя, необходимо учитывать перенос распределяемого вещества в пределах сплошной среды и внутри капли. В этом случае рассчитываются коэффициенты массоотдачи в соответствующих фазах, а затем коэффициент массопередачи по уравнению аддитивности фазовых сопротивлений.
|

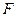 состоит из рас-пределяющей фазы
состоит из рас-пределяющей фазы 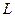 и распределяемого компонента
и распределяемого компонента 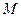 , состав компонента в фазе – x; другая распределяющая фаза представляет – экстрагент
, состав компонента в фазе – x; другая распределяющая фаза представляет – экстрагент 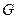 , состав распределяемого компонента в экстрагенте –
, состав распределяемого компонента в экстрагенте –  . Поскольку распределяемый компонент переходит из распределяющей фазы
. Поскольку распределяемый компонент переходит из распределяющей фазы  .
. и
и 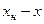 , получим:
, получим: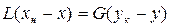 .
.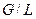 будет переменной величиной. Поэтому рабочая линия процесса экстракции в системе координат
будет переменной величиной. Поэтому рабочая линия процесса экстракции в системе координат 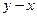 при частичной растворимости фаз не будет прямой линией.
при частичной растворимости фаз не будет прямой линией. ,
,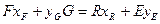 ,
,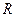 – рафинат, представляет собой исходную смесь после извлечения распределяемого компонента;
– рафинат, представляет собой исходную смесь после извлечения распределяемого компонента; 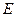 – экстракт представляет собой экстрагент после поглощения распределяемого компонента.
– экстракт представляет собой экстрагент после поглощения распределяемого компонента. . Коэффициент массоотдачи дисперсной фазы может быть рассчитан по уравнениям:
. Коэффициент массоотдачи дисперсной фазы может быть рассчитан по уравнениям: ):
):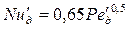
 ,
,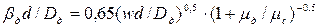 ,
,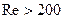 :
:
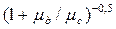 ,
,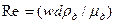 – критерий Рейнольдса;
– критерий Рейнольдса; 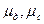 – динамические коэффициенты вязкости дисперсной и сплошной сред, соответственно.
– динамические коэффициенты вязкости дисперсной и сплошной сред, соответственно. 2 и
2 и  200), то процесс массообмена определяется только диффузионным сопротивлением сплошной фазы. В этом случае коэффициент массопередачи может быть принят равным коэффициенту массоотдачи сплошной фазы
200), то процесс массообмена определяется только диффузионным сопротивлением сплошной фазы. В этом случае коэффициент массопередачи может быть принят равным коэффициенту массоотдачи сплошной фазы  . Коэффициент массоотдачи
. Коэффициент массоотдачи 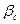 может быть рассчитан по критериальному уравнению:
может быть рассчитан по критериальному уравнению: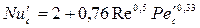
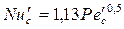 ,
, ,
, – диаметр капли;
– диаметр капли; 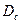 – коэффициент диффузии распределяемого вещества в сплошной фазе;
– коэффициент диффузии распределяемого вещества в сплошной фазе;  – относительная скорость движения капель в сплошной
– относительная скорость движения капель в сплошной 


