Рекомендации по обработке экспериментальных данных. 1. Рассчитать экспериментальное значение коэффициента теплоотдачи (aэксп) по формуле (2.2.2).
1. Рассчитать экспериментальное значение коэффициента теплоотдачи (aэксп) по формуле (2.2.2). Тепловой поток от поверхности трубы к воздуху определяется по формуле:
где ср , G = 1006 Дж/(кг∙К) – удельная теплоёмкость воздуха (практически постоянная в интервале температур 0…90 °С);
Для определения расхода воздуха используются показания дифференциального манометра, соединённого с трубкой Пито-Прандтля, измеряющей локальную (на оси канала) скорость потока. Локальная (осевая, а значит – максимальная) скорость воздуха в трубке определяется по формуле:
где D h м – разность уровней жидкости в коленах дифманометра; rм @ 1000 кг/м3 – плотность манометрической жидкости (воды); rG – плотность воздуха. Если число Рейнольдса
если число Рейнольдса
Массовый расход воздуха в канале
В формулах (2.2.8)…(2.2.11) физические свойства воздуха определяются при конечной его температуре Средняя по длине цилиндра температура поверхности определяется по формуле (2.2.4). Для численного интегрирования может быть использовано соотношение:
где L = 685 мм - расстояние между крайними точками замера температур; Т 2… Т 11 - температуры в локальных точках цилиндра; li - расстояние между соседними локальными точками измерения температуры; на лабораторной установке l 2 = 15 мм, l 3 =40 мм, l 4 =70 мм, l 5 =95 мм, l 6 = l 7 = l 8 = 120 мм, l 9 = 85 мм, l 10 = 20 мм. Примечание: отсчёт номеров точек и длин участков начат с цифры «2», так как именно под этим номером значится первый датчик температуры на поверхности трубки.
Средняя температура воздуха в канале с достаточной точностью может быть определена как среднеарифметическая величина, то есть
где Т G, н и Т G, к – соответственно начальная и конечная температура воздуха в канале.
2. Рассчитать число Рейнольдса, соответствующее установленному расходу воздуха:
и экспериментальное число Нуссельта
В формулах (2.2.14) и (2.2.15) физические свойства воздуха определяются при средней его температуре 3. Полученное экспериментально значение коэффициента теплоотдачи сравнивается со значением, рассчитанным по эмпирическим формулам. При этом могут быть использованы следующие критериальные уравнения:
▫ если 2300 < Re < 10000, то
▫ если Re > 10000, то
Результаты измерений и вычислений занести в таблицы:
Все экспериментальные данные обобщаются и аппроксимируются зависимостью вида (2.2.6).
По полученным значениям экспериментальных и рассчитанных по эмпирическим формулам коэффициентов теплоотдачи, а также по виду (числовым величинам коэффициентов С и п) критериального уравнения формы (2.2.6) сделать соответствующее заключение.
|

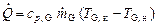 ,
,
 – массовый расход воздуха.
– массовый расход воздуха. ,
,
 < 4500, то средняя скорость воздуха в выходном (конечном) сечении канала
< 4500, то средняя скорость воздуха в выходном (конечном) сечении канала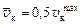 ;
;
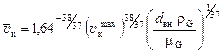 .
.
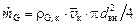 .
.
 .
. ,
,
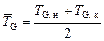 ,
,
 ,
,
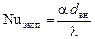 .
.
 .
.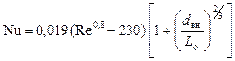 ;
;
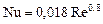 .
.

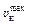 м/с
м/с
 ,
кг/с
,
кг/с
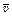 ,
м/с
,
м/с
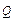 ,
Вт
,
Вт



