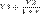Intertemporal choice problem as foundation of the modern theory of finance.

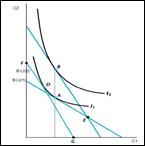
Model of intertemporal choice involving consumption and investment decisions. (Named after Irving Fisher)

Irving Fisher developed the theory of Intertemporal Choice in 1930 in his book 'Theory of interest'. Contrary to Keynes, who related consumption to current income, Fisher’s model showed how rational forward looking consumers chooses consumption for the present and future to maximize their lifetime satisfaction. According to Fisher, an individual's impatience depends on four characteristics of his income stream: the size, the time shape, the composition and risk. Besides this foresight, self control, habit, expectation of life, and bequest motive (or concern for lives of others) are the five personal factors that determine a person's impatience which in turn determines his time preference. In order to understand the choice exercised by a consumer across different periods of time we take consumption in one period as a composite commodity. Suppose there is one consumer, N commodities, and two periods. Preferences are given by U (x1; x2) where xt = (xt1;:::; xtN). Income in period t is Yt. Savings in period 1 is S1, spending in period t is Ct, and r is the interest rate.

C1 + S1 ≤Y1... (1)

C2 ≤ Y2 + S1 (1 + r)... (2)

We arrive at the following equation from equation 1 and 2

= =

The left hand side shows the present value expenditure and right hand side depicts the present value income respectively. Multiplying the equation by (1+r) gives us the future value.

Now the consumer has to choose a C1 and C2 such that Max U(C1,C2) subject to C1+C2/(1+r) = Y1 + Y2/(1+r)

A consumer maybe a net saver or a net borrower. If he's initially at a level of consumption where he's neither of the above(i.e. a net borrower or net saver), an increase in income may make him a net saver or a net borrower depending on his preferences. An increase in current income or future income will increase current and future consumption(consumption smoothing motives).

Now, let us consider a scenario where the interest rates are increased. If the consumer is a net saver, he will save more in the current period due to the substitution effect and consume more in the current period due to the income effect. The net effect thus, becomes ambiguous. If the consumer is a net borrower, however, he will tend to consume less in the current period due to the substitution effect and income effect thereby reducing his overall current consumption.

If the consumer is a net saver, an increase in interest rate will have an ambiguous effect on the current consumption.

 

If the consumer is a net borrower, an increase in interest rate will reduce his current consumption.

 

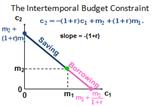
Key Assumptions:

· Two periods (generalizing to many future periods is straightforward); Perfect capital markets; the absence of uncertainty

What is the consumer choosing? One of the many possible “Consumption Streams”. A consumption stream is a sequence of time dated consumption. Consumers are able to choose between alternative consumption streams. Choices are consistent (transitive), they prefer more consumption to less, i.e. they prefer higher standards of living to lower. Consumers choose the most preferred consumption stream among those attainable. Let m₁ and m₂ be incomes received in periods 1 and 2. Let c₁ and c₂ be consumptions in periods 1 and 2. Let p₁ and p₂ be the prices of consumption in periods 1 and 2. Suppose prices are 1$. Suppose that the consumer chooses not to save or to borrow. What will be consumed in period 1? c₁ = m₁. What will be consumed in period 2? c₂ = m₂.

Now suppose that the consumer spends nothing on consumption in period 1; that is, c₁ = 0 and the consumer saves s₁ = m₁. The interest rate is r. What now will be period 2’s consumption level?

Now suppose that the consumer spends everything possible on consumption in period 1, so c₂ = 0. What is the most that the consumer can borrow in period 1 against her period 2 income of $m₂? Let b₁ denote the amount borrowed in period 1. Only $m₂ will be available in period 2 to pay back $b₁ borrowed in period 1. So b₁(1 + r) = m₂. That is, b₁ = m₂ / (1 + r). So the largest possible period 1 consumption level is.

The calculation of saving or borrowing amounts is the modern theory of finance. All these calculation used in calculation of investing or spending cash flows. For example, bond, securities etc.
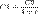