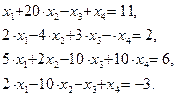Повна похибка розв’язку задачі на комп’ютері: неусувна, методу, заокруглювання.
ЕКЗАМЕНАЦІЙНІ БІЛЕТИ
До семестрового контролю З дисципліни "ЧИСЕЛЬНІ МЕТОДИ В ІНФОРМАТИЦІ" Освітньо-кваліфікаційний рівень бакалавр
Підготовлені доц. Людвиченком В.О.
Четвертий курс
Повна похибка розв’язку задачі на комп’ютері: неусувна, методу, заокруглювання. 2. Алгоритм методу Ньютона обчислення коренів системи нелінійних рівнянь. 3. Методом Ньютона «вручну» (та використовуючи пакет MATLAB) знайти з точністю
виходячи із початкового наближення
…………………………………………………… 1. Інтерполяція функцій, заданих своїми значеннями в точках, сплайнами (лінійним, квадратичним). 2. Апроксимація функцій, заданих своїми значеннями в точках, методом найменших квадратів. 3. Використовуючи метод найменших квадратів (та з допомогою пакету MATLAB) знайти коефіцієнти параболи
1. Наближення функцій, заданих своїми значеннями в точках, кубічним інтерполяційним сплайном. 2. Метод простих ітерацій розв’язування системи лінійних алгебраїчних рівнянь (СЛАР). 3. Методом простої ітерації «вручну» (та використовуючи пакет MATLAB) знайти із точністю
виходячи із початкового наближення
1. Метод Гауса розв’язування системи лінійних алгебраїчних рівнянь (СЛАР). 2. Наближення функцій, заданих своїми значеннями в точках, квадратичним інтерполяційним сплайном. 3. Знайти «вручну» (і використовуючи пакет MATLAB) квадратичний інтерполяційний сплайн, який проходить через точки (-3;2), (-2;0), (1;1), (4;1) і з граничною умовою: 1. Метод Ньютона обчислення коренів системи нелінійних рівнянь із заданою точністю по нев’язці ( 2. Метод Гауса розв’язування системи лінійних алгебраїчних рівнянь (СЛАР). 3. Розв'язати «вручну» методом Гауса (і використовуючи пакет MATLAB) систему лінійних алгебраїчних рівнянь:
1. Інтерполяція функцій, заданих своїми значеннями в точках: інтерполяційний многочлен Лагранжа. 2. Метод Ейлера для розв’язування ЗДР. 3. Знайти «вручну» методом Ейлера (та використовуючи пакет MATLAB) на відрізку 1. Алгоритм методу ділення відрізку пополам обчислення коренів нелінійних рівнянь із заданою точністю ( 2. Метод Гауса розв’язування системи лінійних алгебраїчних рівнянь. 3. Розв’язати «вручну» методом Гауса (та використовуючи пакет MATLAB) систему лінійних алгебраїчних рівнянь:
__________________________________________ 1. Розв’язування системи лінійних алгебраїчних рівнянь методом ітерацій Зейделя. 2. Метод Ньютона (дотичних) обчислення коренів нелінійних рівнянь з заданою точністю ( 3. Знайти методом Ньютона (та використовуючи пакет MATLAB) корінь рівняння
з точністю 1. Метод Ейлера для розв’язування звичайних диференціальних рівнянь (ЗДР). 2. Розв’язування системи лінійних алгебраїчних рівнянь методом ітерацій Зейделя 3. Розв’язати «вручну» ітераційним методом Зейделя (та використовуючи пакет MATLAB) систему лінійних алгебраїчних рівнянь:
------------------------------------------------------------ 1. Апроксимація функцій, заданих своїми значеннями в точках, методом найменших квадратів. 2. Метод Рунге-Кутта для розв’язування звичайних диференціальних рівнянь (ЗДР). 3. Знайти «вручну» методом Рунге-Кутта (та використовуючи пакет MATLAB) на відрізку
1. Метод Ейлера для розв’язування звичайних диференціальних рівнянь (ЗДР). 2. Апроксимація функцій, заданих своїми значеннями в точках, методом найменших квадратів. 3.Використовуючи метод найменших квадратів (та з допомогою пакету MATLAB) знайти коефіцієнти параболи
-------------------------------------------------------------------- 1. Розв’язування системи лінійних алгебраїчних рівнянь методом Гаусса з вибором головного елемента. 2. Інтерполяція функцій, заданих своїми значеннями в точках: інтерполяційний многочлен Лагранжа.
1. Розв’язування системи лінійних алгебраїчних рівнянь методом Гаусса. 2. Метод поділу навпіл (бісекцій, або дихотомії) обчислення коренів нелінійних рівнянь з заданою точністю ( 3. Знайти «вручну» методом дихотомії (половинного ділення) (та використовуючи пакет МАTLAB) корінь рівняння
з точністю ------------------------------------------------------------------------ 1. Метод Гауса розв’язування системи лінійних алгебраїчних рівнянь (СЛАР). 2. Наближення функцій, заданих своїми значеннями в точках, квадратичним інтерполяційним сплайном. 3. Знайти «вручну» (і використовуючи пакет MATLAB) квадратичний інтерполяційний сплайн, який проходить через точки (-3;2), (-2;0), (1;1), (4;4) і з граничною умовою: 1. Метод Ньютона обчислення коренів нелінійних рівнянь з заданою точністю ( 2. Обчислення означених інтегралів із заданою точністю з використанням методу Сімпсона (парабол). 3. Обчислити «вручну» по формулі Сімпсона (та використовуючи пакет МАTLAB) інтеграл --------------------------------------------------------------------------- 1. Метод градієнтного спуску мінімізації випуклої функції багатьох змінних. 2. Інтерполяція функцій, заданих своїми значеннями в точках: інтерполяційний многочлен Лагранжа. 3. Розв’язати «вручну» (та використовуючи пакет МАTLAB) задачу інтерполяції за допомогою многочленна Лагранжа для функції
1. Алгоритм методу простих ітерацій обчислення коренів нелінійних рівнянь із заданою точністю ( 2. Метод Гауса розв’язання системи лінійних алгебраїчних рівнянь. 3. Розв’язати «вручну» методом Гауса (та використовуючи пакет MATLAB) систему лінійних алгебраїчних рівнянь:
----------------------------------------------------------------- 1. Метод мінімізації випуклої функції багатьох змінних по випадковому напрямку спуску. 2. Обчислення означених інтегралів із заданою точністю з використанням методу прямокутників. 3. Обчислити «вручну» (та використовуючи пакет МАTLAB) інтеграл
по формулі прямокутників із заданою відносною точністю
1. Обчислення означених інтегралів із заданою точністю з використанням методу трапецій. 2. Розв’язування системи лінійних алгебраїчних рівнянь методом простої ітерації. 3. Розв'язати «вручну» методом простої ітерації (та використовуючи пакет MATLAB) систему лінійних алгебраїчних рівнянь:
------------------------------------------------------------------- 1. Інтерполяція функцій, заданих своїми значеннями в точках, сплайнами. 2. Апроксимація функцій, заданих своїми значеннями в точках, методом найменших квадратів. 3. Використовуючи метод найменших квадратів (та з допомогою пакету MATLAB) знайти коефіцієнти параболи
1. Метод Гауса розв’язування системи лінійних алгебраїчних рівнянь (СЛАР). 2. Наближення функцій, заданих своїми значеннями в точках, квадратичним інтерполяційним сплайном. 3. Знайти «вручну» (і використовуючи пакет MATLAB) квадратичний інтерполяційний сплайн, який проходить через точки (-3;2), (-2;0), (1;1), (4;1) і з граничною умовою: 1. Алгоритм методу поділу відрізка пополам.обчислення коренів нелінійних рівнянь із заданою точністю (
1. Інтерполяція функцій, заданих своїми значеннями в точках, сплайнами. 2. Метод сіток розв’язання крайових задач для диференціальних рівнянь еліптичного типу. 3. Знайти «вручну» (і використовуючи пакет MATLAB) квадратичний інтерполяційний сплайн, який проходить через точки (0;2), (1;1), (2;4), (3;3) і з граничною умовою:
1. Метод покоординатного спуску мінімізації випуклої функції багатьох змінних. 2. Метод сіток розв’язання крайових задачі для диференціальних рівнянь гіперболічного типу. 3. Розв'язати «вручну» методом Гауса (та використовуючи пакет MATLAB) систему лінійних алгебраїчних рівнянь:
1. Метод штрафних функцій для умовної мінімізації випуклої функції багатьох змінних. 2. Метод сіток розв’язання крайових задачі для диференціальних рівнянь параболічного типу. 3. Знайти «вручну» (та використовуючи пакет MATLAB) квадратичний інтерполяційний сплайн, який проходить через точки (0;0), (1;1), (2;4), (3;2) і з граничною умовою для першої похідної: ------------------------------------------------------------- 1. Метод штрафних функцій для умовної мінімізації випуклої функції багатьох змінних. 2. Метод Ейлера для розв’язування звичайних диференціальних рівнянь (ЗДР). 3..Знайти «вручну» методом Ейлера (та використовуючи пакет MATLAB) на відрізку 1. Метод градієнтного спуску мінімізації випуклої функції багатьох змінних. 2. Метод Гауса розв’язування системи лінійних алгебраїчних рівнянь (СЛАР). 3. Розв’язати «вручну» методом Гауса (та використовуючи пакет MATLAB) систему лінійних алгебраїчних рівнянь:
---------------------------------------------------------------
1. Інтерполяція функцій, заданих своїми значеннями в точках, сплайнами. 2. Метод Ньютона обчислення коренів нелінійних рівнянь з заданою точністю ( 3. Знайти «вручну» методом Ньютона (та використовуючи пакет MATLAB) корінь рівняння з точністю початкового наближення
1. Апроксимація функцій, заданих своїми значеннями в точках, методом найменших квадратів. 2. Метод Ейлера для розв’язування звичайних диференціальних рівнянь (ЗДР). 3. 3найти «вручну» методом Ейлера (та використовуючи пакет MATLAB) на відрізку
|

 по нев’язці корінь системи рівнянь
по нев’язці корінь системи рівнянь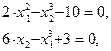
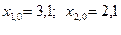 .
.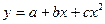 , яка апроксимує дані, що представлені таблицею:
, яка апроксимує дані, що представлені таблицею:
 .
.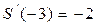 .
.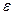 -коренів).
-коренів).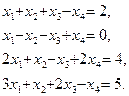
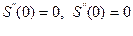 .
.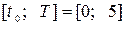 розв’язок задачі Коші для диференціального рівняння
розв’язок задачі Коші для диференціального рівняння 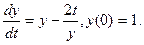 Вибрати крок
Вибрати крок  .
.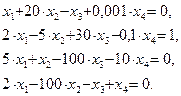
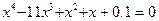
 по нев’язці, виходячи із початкового наближення
по нев’язці, виходячи із початкового наближення 
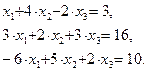
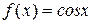 , таблично заданою в восьми точках на інтервалі
, таблично заданою в восьми точках на інтервалі  .
. 
 із заданою відносною точністю
із заданою відносною точністю 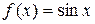 , таблично заданої в восьми точках на інтервалі
, таблично заданої в восьми точках на інтервалі 


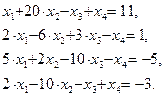
 .
. .
.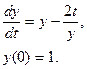 Вибрати крок
Вибрати крок