Теорема ТейлораПусть функция
Без доказательства. Замечание. При п =0 получаем частный случай - формулу Лагранжа:
Таким образом, можно сказать, что формула Тейлора есть обобщение формулы Лагранжа на случай п производных. Формула (2.7.1) называется формулой Тейлора, а последнее слагаемое в ней - остаточным членом в форме Лагранжа. Таким образом,
Приведем еще одну форму записи остаточного члена - в форме Пеано (Пеано Джузеппе, Peano, 1858-1932).
Тогда формула Тейлора примет вид:
При
Остаточный член имеет вид: 1) в форме Лагранжа 2) в форме Пеано
|
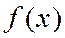имеет в точке а и некоторой её окрестности производные порядка п +1. Пусть х - любое значение аргумента из указанной окрестности, 
. Тогда между точками а и х найдется точка x такая, что справедлива следующая формула:
(2.7.1)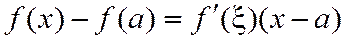
.
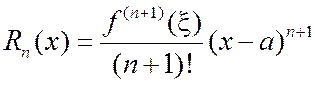. (2.7.2)
при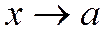 
. (2.7.3)
.
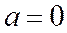формула Тейлора (2.7.1) превращается в формулу Маклорена:
(2.7.4)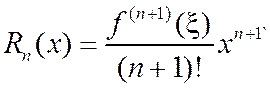
;
.
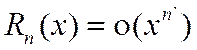