В степенной ряд
Если функция
то это разложение единственно. Доказательство. По условию ряд сходится на интервале Дифференцируя, получаем:
…………………………………………………………
Здесь нужно заметить, что в свободных членах индексы и факториалы имеют п -й порядок, т.е. тот же порядок, что и производная, а при х в первой степени(п +1)-й порядок. Полагая в полученных равенствах и в равенстве (2.6.4)
Таким образом, все коэффициенты ряда (2.6.1) определяются единственным образом формулами (2.6.2), что и доказывает теорему. Подставляя полученные выражения коэффициентов в равенство (2.6.1), получаем:
Итак, если функция Если функция разлагается в ряд вида (2.5.3), то соответствующий ряд
называется рядом Тейлора. Таким образом, ряд Маклорена является частным случаем ряда Тейлора, когда Формально ряды Тейлора и Маклорена можно составить для любой функции, имеющей производные любого порядка, и для любой точки из области дифференцируемости, однако полученные ряды не обязательно будут сходиться к этой функции; они могут вообще расходиться. Поэтому, составив такой ряд, вначале не ставят знака равенства между функцией и рядом, а заменяют его знаком соответствия "~":
Говорят, что функция 1) на этом интервале ряд сходится; 2) сумма ряда
|

 на интервале
на интервале  разлагается в степенной ряд
разлагается в степенной ряд , (2.6.1)
, (2.6.1) и функция
и функция  - его сумма. Следовательно, по теореме о дифференцировании степенных рядов ряд (2.6.1) можно почленно дифференцировать на интервале
- его сумма. Следовательно, по теореме о дифференцировании степенных рядов ряд (2.6.1) можно почленно дифференцировать на интервале 
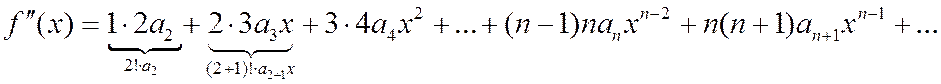


 , имеем:
, имеем: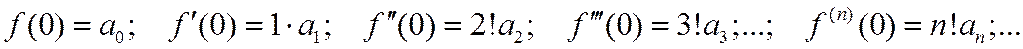 Отсюда
Отсюда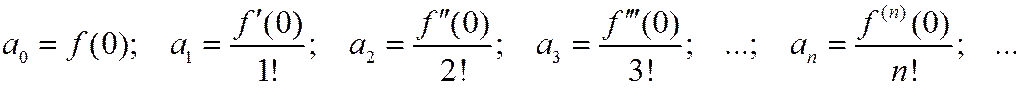 (2.6.2)
(2.6.2)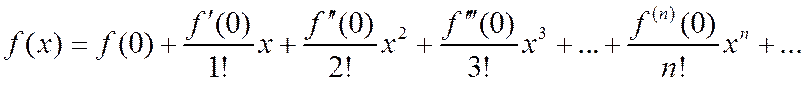 (2.6.3)
(2.6.3) разлагается в степенной ряд, то этот ряд имеет вид (2.6.3), который называется рядом Маклорена для функции
разлагается в степенной ряд, то этот ряд имеет вид (2.6.3), который называется рядом Маклорена для функции 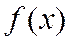 .
.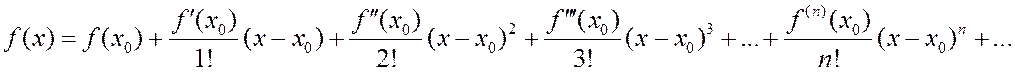 (2.6.4)
(2.6.4)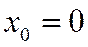 .
.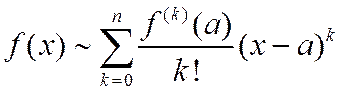 .
.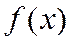 разлагается в ряд Тейлора на интервале (a-R, a+R), если выполняются два условия:
разлагается в ряд Тейлора на интервале (a-R, a+R), если выполняются два условия: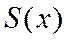 равна функции
равна функции 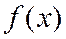 . В этом, и только в этом случае пишут знак равенства "=" вместо знака соответствия "~" между
. В этом, и только в этом случае пишут знак равенства "=" вместо знака соответствия "~" между 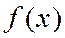 и рядом, т. е.
и рядом, т. е. . (2.6.5)
. (2.6.5)


