Припустимо, що на деякій території мешкають два види тварин: кролики (харчуються рослинами) і лисиці (харчуються кроликами). Нехай число кроликів 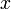 , Число лис
, Число лис 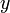 .Використовуючи Модель Мальтуса з необхідними поправками, що враховують поїдання кроликів лисицями, приходимо до наступного системі, що носить ім'я моделі Вольтерра - Лотки:
.Використовуючи Модель Мальтуса з необхідними поправками, що враховують поїдання кроликів лисицями, приходимо до наступного системі, що носить ім'я моделі Вольтерра - Лотки:
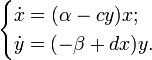
Ця система має рівноважний стан, коли число кроликів і лисиць постійно. Відхилення від цього стану призводить до коливань чисельності кроликів і лисиць, аналогічним коливаннямгармонійного осцилятора. Як і у випадку гармонійного осцилятора, це поведінка не є структурно стійким: мале зміна моделі (наприклад, що враховує обмеженість ресурсів, необхідних кроликам) може привести до якісної зміни поведінки. Наприклад, рівноважний стан може стати стійким, і коливання чисельності будуть затухати. Можлива і протилежна ситуація, коли будь-яке мале відхилення від положення рівноваги призведе до катастрофічних наслідків, аж до повного вимирання одного з видів. На питання про те, який з цих сценаріїв реалізується, модель Вольтерра - Лотки відповіді не дає: тут потрібні додаткові дослідження.
З точки зору теорії коливань модель Вольтерра - Лотки є консервативною системою, має перший інтегралом руху. Ця система не є грубою, оскільки найменші зміни правій частині рівнянь призводять до якісних її змін динамічного поведінки. Однак, можливо "злегка" модифіковані праву частину рівнянь таким чином, що система стане автоколебательной.Наявність стійкого граничного циклу, властивого грубим динамічним системам, сприяє значному розширенню області застосування моделі

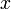 , Число лис
, Число лис 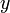 .Використовуючи Модель Мальтуса з необхідними поправками, що враховують поїдання кроликів лисицями, приходимо до наступного системі, що носить ім'я моделі Вольтерра - Лотки:
.Використовуючи Модель Мальтуса з необхідними поправками, що враховують поїдання кроликів лисицями, приходимо до наступного системі, що носить ім'я моделі Вольтерра - Лотки: