Модель багатовидової популяції
Наступною ланкою в ієрархічному ланцюзі є перехід до моделі багатовидової популяції. Розглянемо таку модель, а також укажемо на задачі, пов’язані з нею. Розв’язання таких задач може стати темою подальших наукових досліджень і кваліфікаційних робіт різного рівня. Нехай
де Аналогічно можна переконатися, що перший квадрант є фазовим простором даної системи. При її дослідженні (навіть у випадку сталих коефіцієнтів) виникає низка серйозних математичних проблем, відповідь на які потрібно отримати в термінах коефіцієнтів системи, тобто функцій 1. Дослідити умови конкурентного зникнення одного чи кількох видів, тобто умови, за яких 2. Знайти умови обмеженості числа особин певного виду, тобто 3. Знайти умови періодичності зміни числа особин 4. Дослідити умови перманентності системи (2.1.14). Останнє означає існування в першому квадранті деякої компактної множини З погляду біологічних популяцій, умови перманентності означають умови “мирного” співіснування всіх видів, коли жоден з видів не зникає.
|
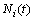– кількість особин і-го виду 
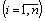. Математичною моделлю їх співіснування є узагальнення моделі Лотки – Вольтерра на 
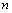рівнянь
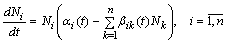, (2.1.14)
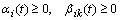– коефіцієнти системи.
і 
:
при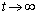 
для деяких 
.
щоб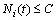 
для деяких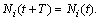 
, що має таку властивість: усі розв’язки системи (2.1.14), починаючи з деякого моменту часу (для кожного розв’язку – свого), лежать у даній множині.
