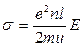Вынужденные колебания в электрическом колебательном контуре. Резонанс. Резонансные кривые.
Чтобы в реальной электрическом колебательном контуре получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью вынуждающей силы - внешней эдс, изменяющейся по гармоническому закону: U = Um cos wt. Согласно второму правилу Кирхгофа, для контура, содержащего катушку индуктивностью L, конденсатор емкостью С и резистор R и в котором действует внешняя эдс можно записать
где Uc = = q/C — напряжение на конденсаторе, es - э.д.с. самоиндукции, возникающая в катушке при протекании в ней переменного тока, IR – падение напряжения на сопротивлении. Следовательно, уравнение (2) можно привести к виду
или разделив на L при учете, что I=dq/dt, а dI/dt=d2q/dt2 получим дифференциальное уравнение колебаний заряда q в контуре или дифференциальное уравнение свободных затухающих колебаний заряда q в контуре:
Такое уравнение известно из курса механики
Здесь b- коэффициент затухания, w0 - циклическая частота собственных колебаний.
В установившемся режиме вынужденные колебания происходят с частотой w и являются гармоническими. Решение уравнения (3) для установившегося режима имеет вид
Причем амплитуда A и фаза j зависят от w, w0, b, x 0
В соответствии с этими формулами для (2) запишем
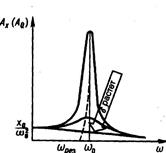
Амплитудные резонансные кривые построенные на основе (4), приведены на рис.1. Явление резкого возрастания амплитуды вынужденных колебаний на некоторой частоте, называемой резонансной (которая для малого затухания совпадает с частотой собственных колебаний w0) называется резонансом.
Рис.1. Чем больше коэффициент затухания, тем ниже амплитуда при резонансе. Статическое отклонение (при w стремящейся к нулю) равно Ares=QAst,, где Фазовая резонансные кривые построенные на основе (5), приведены на рис.2.
Рис.2. Видно, что только в случае когда затухания нет (b=0), вынуждающая сила и колебания совпадают по фазе. Явления резонанса могут быть как вредными, так и полезными. Например, при конструировании машин и различного рода сооружений необходимо, чтобы собственная частота колебаний их не совпадала с частотой возможных внешних воздействий, в противном случае возникнут вибрации, которые могут вызвать серьезные разрушения. С другой стороны, наличие резонанса позволяет обнаружить даже очень слабые колебания, если их частота совпадает с частотой собственных, колебаний прибора. Так, радиотехника, прикладная акустика, оборудование, воспринимающее электрические колебания, основаны на явлении резонанс.
52. Элементарная классическая теория электропроводности металлов (теория Друде – Лоренца)
Элементарная классическая теория электропроводности металлов основана на представлении, что в узлах кристаллической решетки располагаются ионы металла, а между ними хаотически движутся свободные электроны, образуя своеобразный электронный газ, обладающий свойствами идеального газа. Электроны проводимости при своем движении сталкиваются с ионами решетки, в результате чего устанавливается тепловое равновесие между электронным газом и решеткой. По теории Друде — Лоренца, электроны обладают такой же энергией теплового движения, как и молекулы одноатомного газа. Поэтому, применяя выводы молекулярно-кинетической теории (см. (44.3)), можно найти среднюю скорост ь теплового движения электронов При наложении внешнего электрического поля на металлический проводник, кроме теплового движения электронов, возникает их упорядоченное движение, т. е. возникает электрический ток. Среднюю скорость < v > упорядоченного движения электронов можно оценить для плотности тока: j = ne(v). Даже при очень больших плотностях тока средняя скорость упорядоченного движения электронов, обусловливающая электрический ток, значительно меньше их скорости теплового движения. Выведем закон Ома из классической теории металлов. Пусть в металлическом проводнике существует электрическое поле напряженностью Е = const. Co стороны поля заряд е испытывает действие силы F = еЕ и приобретает ускорение а = F/m= еЕ/т. Таким образом, во время свободного пробега электроны движутся равноускоренно, приобретая к концу свободного пробега скорость
где t— среднее время между, двумя последовательными соударениями электрона с ионами решетки. Согласно теории Друде, в конце свободного пробега электрон, сталкиваясь с ионами решетки, отдает им накопленную в поле энергию, поэтому скорость его упорядоченного движения становится равной нулю. Следовательно, средняя скорость направленного движения электрона
Классическая теория металлов не учитывает распределения электронов по скоростям, поэтому среднее время свободного пробега t определяется средней длиной свободного пробега l и средней скоростью движения электронов относительно кристаллической решетки проводника, равной u + v (u — средняя скорость теплового движения электронов, которая значительно больше скорости направленного движения v), поэтому получим t= l / u Подставив значение t в формулу (2), получим
С учетом (3) плотность тока в металлическом проводнике будет равна
откуда видно, что плотность тока пропорциональна напряженности поля, т. е. получили закон Ома в дифференциальной форме. Коэффициент пропорциональности между j и Е является удельной проводимостью материала
которая тем больше, чем больше концентрация свободных электронов и средняя длина их свободного пробега.
|

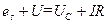 или
или  (1)
(1) ,
,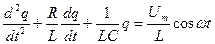 (2)
(2) (3)
(3)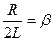 ,
, 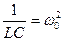 .
.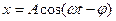 .
. ,
, 

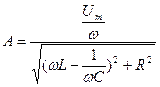 (4)
(4)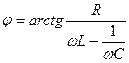 (5)
(5)
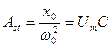 , а амплитуда при резонансе
, а амплитуда при резонансе  , т.е. они связаны через добротность Q
, т.е. они связаны через добротность Q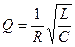 . Чем выше добротность контура, тем выше амплитуда при резонансе.
. Чем выше добротность контура, тем выше амплитуда при резонансе.
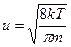 которая для Т = 300 К равна 1,08-105 м/с. Тепловое движение электронов, являясь хаотическим, не может привести к возникновению тока.
которая для Т = 300 К равна 1,08-105 м/с. Тепловое движение электронов, являясь хаотическим, не может привести к возникновению тока.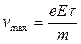 (1),
(1),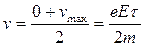 (2)
(2) . (3)
. (3)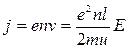 .
.