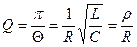Свободные затухающие колебания
Если в контуре присутствует сопротивление R то на нем выделяется тепло согласно закону Джоуля – Ленца и колебания становятся затухающими. Согласно второму правилу Кирхгофа, для контура, содержащего катушку индуктивностью L, конденсатор емкостью С и резистор R можно записать
где Uc = = q/C — напряжение на конденсаторе, es - э.д.с. самоиндукции, возникающая в катушке при протекании в ней переменного тока, IR – падение напряжения на сопротивлении. Следовательно, уравнение (4) можно привести к виду
или разделив на L при учете, что I=dq/dt, а dI/dt=d2q/dt2 получим дифференциальное уравнение колебаний заряда q в контуре или дифференциальное уравнение свободных затухающих колебаний заряда q в контуре:
Они происходит с собственной частотой Здесь Решение данного уравнения имеет вид Колебания происходят с частотой Если w0<b, то колебания прекращаются Время релаксации колебаний Логарифмический декремент затухания имеет вид Добротность контура
|
или 
(4)
,
(5)
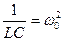, а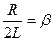 
- коэффициент затухания.
, т.е. амплитуда колебаний заряда уменьшается по экспоненциальному закону.
.
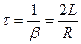