Соединение конвейерных ступеней.

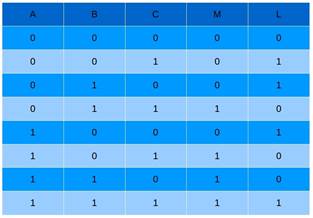
S418

Элементарной, но не тривиальной ступенью, на которой базируется множество арифметических конвейеров, является устройство с тремя двоичными входами и двумя двоичными выходами, суть – двоичная сумма входов.

В зависимости от подключения это устройство может являться либо одноразрядным комбинационным сумматором, либо одноразрядным сумматором с экономией переносов.

S419

 

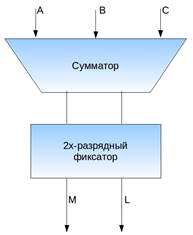
Стандартное обозначение:

 

 

 

S420

На следующих двух схемах показано применение подобного устройства для построения конвейерного сумматора и конвейерного умножителя на основе последовательного переноса.

S421

Оба эти конвейера узко однофункциональны. А как сделать хотя бы простой многофункциональный конвейер?

Для этого необходимо построить многофункциональную вычислительную ячейку и универсальную ячейку управления. Например, такие:

S422

Далее на рисунке показан пример комбинации ячеек, чтобы выполнять умножение, деление, возведение в квадрат и извлечение квадратного корня:

 

 

S423

 

 

 

S424

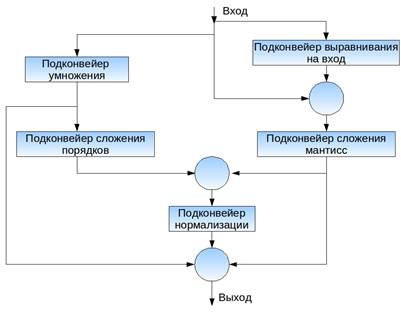
S425

Дальнейшим развитием многофункционального конвейера будет конвейер с множественными путями (ветвящийся). Приведем относительно простой пример: конвейер для умножения чисел с плавающей запятой.

S426

Обобщенно показан многофункциональный конвейер на 4 операции.

В полном соответствии с теорией возникают структурные помехи (столкновения) между различными инициализациями.

Например, пусть за операцией сложения чисел с ПЗ через короткое время пойдет операция сложения чисел с ФЗ. Если не предусмотреть специально взаимную синхронизацию, то подконвейер сложения мантисс две операции попытаются использовать одновременно.

S427

Следующий шаг в развитии конвейеров – конвейеры с обратной связью. Они могли бы применяться для обработки рекурсий. Сюда может быть отнесено много задач обработки сигналов с обобщенной формулой:

x (i) = f (a (i), x (i-1), …, x (i-m)), где, например,

a (i) – i-й раз измеренное значение входного сигнала;

x (i) – соответствующее значение результата вычислений.

Попытаемся напрямую построить схему конвейера:

S428

Проанализируем работу такой схемы: если число ступеней для вычисления f равно d, то время от начала вычисления x(i) до завершения составит d периодов синхронизации; а поскольку x(i+1) зависит от x(i), то до завершения вычисления x(i) нельзя начать вычисления x(i+1). Конвейерность исчезла!

Существуют способы повышения производительности с помощью «опорного преобразователя», так называемая «каскадная реализация» и других экзотических инженерных решений, но все это будет связано с резким ростом аппаратных затрат.