Функция принадлежности на универсальной шкале
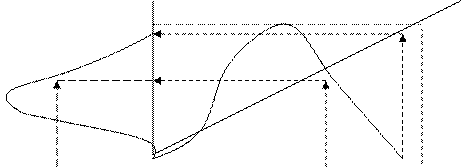
Обычно функции принадлежности формируются на основе данных, получаемых от специалистов в моделируемой предметной области (экспертов). При этом функция принадлежности строится на предметной шкале. Если пределы универсального множества Х изменяются, придется вновь прибегать к опросу экспертов для построения функций принадлежности. Для некоторых задач можно избежать этого этапа с помощью использования универсальных шкал. Для этого используется преобразование, отображающее значения функции принадлежности на отрезок [0;1]. Такое преобразование, в свою очередь, представляет собой некоторую функцию, которая строится также с помощью экспертов. При грубом приближении в качестве этой функции можно использовать прямую (f на рис.8). Функции принадлежности на универсальной шкале изображается вертикально. Значения, расположенные на оси Х, отображаются с помощью функции f на вертикальную ось, отрицательная часть горизонтальной оси превращается в ось значений функции принадлежности. Так в примере на рис.8 функции приведено отображение функций принадлежности на универсальную шкалу. В этом случае при изменении границ универсального множества достаточно выполнить обратное преобразование для получения функций принадлежности в новых границах, не привлекая вновь к этой процедуре экспертов.
f
a
Рис.8. Функция принадлежности на универсальной шкале Нечеткая переменная – это тройка <a, X,Ca>, где a – наименование нечеткой переменной, X – универсальное множество, Ca – нечеткое множество, определенное на множестве X.
|

 1 1
1 1 1 a 0 Х1
1 a 0 Х1


