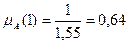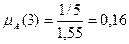Формирование функции принадлежности

При построении функций принадлежности используются мнения экспертов в предметной области.

Классификация методов формирования функции принадлежности.

Все методы формирования функций принадлежности делятся на методы, в которых участвует один эксперт и методы, в которых обрабатываются мнения группы экспертов. При этом в каждом классе методов выделяются прямые и косвенные методы.

В прямых методах значения степени принадлежности назначаются непосредственно самими экспертами либо эксперты сообщают способ вычисления значений функции принадлежности.

В косвенных методах осуществляется сравнительная оценка вариантов. В этом случае для построения функции принадлежности формируется матрица парных сравнений М. Элементы m_{i j} матрицы М показывают, во сколько раз, по мнению эксперта, m_А(х _i) больше, чем m_А(х _j).

Рассмотрим подробнее все методы.

1) Прямой метод с одним экспертом. В этом случае эксперта просят непосредственно дать оценку функции принадлежности.

2) Прямой метод с несколькими экспертами. Один из простейших методов, в котором используется мнение нескольких экспертов. Каждый из них отвечает на прямой вопрос: «Соответствует ли значение х_i оцениваемому понятию?”. Допускаются ответы «Да» или «Нет». Пусть n₁ экспертов дают положительный ответ на вопрос о принадлежности элемента Х = { 10, 11, 12,…,40 } нечеткому множеству А, а n₂ - отрицательный. Тогда за значение m_А(х _i) принимается отношение n₁ / (n₁ + n₂).

ПРИМЕР. Пусть в опросе участвовали 10 экспертов. Оценивались элементы универсального множества Х = {10, 20, 30,…,100} на принадлежность нечеткому множеству, формализующему понятие «Малая скорость автомобиля».

Получены следующие результаты (таблица 1).

 

Таблица 1

Значения хi
Число положительных ответов
Число отрицательных ответов

Таким образом, имеем:

m_А( 10 ) =1; m_А( 20 ) = 0,9; m_А( 30 ) =0,6; m_А( 40 ) =0,4; m_А( 50 ) =0,3; m_А( 60 ) =0;

m_А( 70 ) =0; m_А( 80 ) =0; m_А( 90 ) =0; m_А( 100 ) =0.

 

3) Косвенный метод с одним экспертом. Косвенные методы используются обычно в случаях, когда трудно или невозможно использовать количественную оценку для элементов х_i . Тогда высказывается мнение о предпочтительности вариантов. Один из подходов следующий. Эксперту задаются вопросы: что лучше соответствует понятию х_i или х_j. В результате формируется матрица парных сравнений М = { m _{i j}} i,j = 1,n, где n – количество элементов универсального множества.

Значения m _{i j} формируются с использованием следующей шкалы:

1, если m_А(х_i) и m_А(х_j) примерно равны, т.е. элементы х_i и х_j имеют одинаковую значимость;

3, если m_А(х_i) немного больше, чем m_А(х_j), т.е. существуют малоубедительное предпочтение;

5, если m_А(х_i) больше, чем m_А(х_j), т.е. имеются доказательства превосходства;

7, если m_А(х_i) заметно больше, чем m_А(х_j), т.е. можно привести убедительные свидетельства очевидного превосходства х_i;

9,если m_А(х_i) намного больше, чем m _А(х_j), значит эксперт убежден в абсолютном превосходстве х_i.

Возможны промежуточные значения, 2, 4, 6, 8, в случае более уточненных оценок, даваемых экспертом. Так m_{i j} = 5 означает, что элемент х _i лучше, чем х _j соответствует понятию, описываемому нечетким множеством, для которого строится функция принадлежности. На элементы матрицы парных _i сравнений накладываются требования согласованности: m_ii = 1 и m_ii = 1/ m _{i j}.

Далее осуществляется обработка элементов матрицы. Один из подходов – следующий:

m_А(х_i) = m_{i j} / å _i m _{i j}.

При использовании данного метода m_А(х_i)>;1. Такая функция называется ненормированной. Чтобы добиться m_А(х_i)<;1, результаты расчетов нормируются:

m_А(х_i)= m_А(х_i) / max{m_А(х_i)}.

При этом в качестве j может быть выбрано любое значение от 1 до n, т.е. при правильно проведенном опросе выбор столбца матрицы М не влияет на правильное определение значений функции принадлежности.

ПРИМЕР. Пусть в результате опроса экспертов получена матрица М:

Тогда, вычисляя m_А(х_i) первым способом, получим:

A={<0,64/1>, <0,16/3>, <0,11/6>, <0,09/8>}

Нормируем функцию

A={<1/1>, <0,26/3>, <0,17/6>, <0,14/8>}