Нечеткие множества. Пусть Х – множество некоторых объектов х, соответствующих некоторому понятию: Х={х} называютуниверсальным множеством
Пусть Х – множество некоторых объектов х, соответствующих некоторому понятию: Х={х} называютуниверсальным множеством. Нечетким (расплывчатым) множеством А, соответствующим заданному понятию, назовем множество пар А = { < mА(х) / х>;}, где х Î Х, а mА(х) - функция принадлежности (степень принадлежности), mА(х) Î [0,1]. mА(х) - субъективная мера того, насколько элемент х множества Х соответствует понятию, формализуемому с помощью нечеткого множества А. Если множество Х представить как множество действительных чисел, получим непрерывную функцию принадлежности. SA={x | xÎX & mА(х)>0} – носитель нечеткого множества.
ПРИМЕР. Имеется универсальное множество X={5,10,15,…,40}, соответствующее понятию детский возраст. Найдем нечеткое множество и построим функцию принадлежности. А={<1/5>, <1/10>, <0,6/15>, <0,3/20>, <0/25>, <0/30>, <0/35>, <0/40>}. Графическое представление функции принадлежности показано на рис.2.
1 mА(х) функция принадлежности
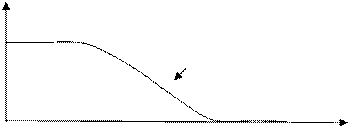
5 10 15 20 25 30 35 40 x Рис.2. Пример построения функции принадлежности. Если Х – непрерывно, то переходим к непрерывному варианту и получаем функцию принадлежности. В большинстве случаев функции принадлежности строятся субъективно по результатам опроса экспертов, поэтому они являются в некотором смысле «приближенными», т.е. не абсолютно адекватно отражающими явление или объект. Собственно говоря, из субъективности следует, что абсолютной адекватности не существует в принципе. Поэтому, нужно выбирать такую функцию, с которой можно было бы как можно проще вести расчеты. Такими функциями являются трапециевидные функции (рис.3). Тогда mА(u) характеризуется четверкой (
Рис.3. Трапециевидная функция принадлежности
|

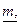
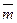 ,
, 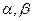 ). Как частный случай при
). Как частный случай при  имеем треугольную форму трапеции.
имеем треугольную форму трапеции.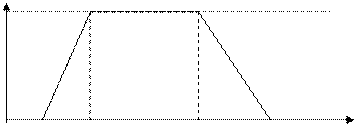 mА(u)
mА(u)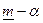
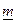
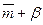 u
u


