Операции над нечеткими множествами. Пусть имеем нечеткие множества А и В на универсальном множестве Х с функциями принадлежности mА(х) и mВ(х).
Пусть имеем нечеткие множества А и В на универсальном множестве Х с функциями принадлежности mА(х) и mВ(х). 1) Дополнение – это нечеткое множество с функцией принадлежности
m
х Рис.4. Операция дополнения 2) Объединение – это нечеткое множество с функцией принадлежности mАÈB(х)=max(mА(х), mВ (х)), " х Î Х.
х
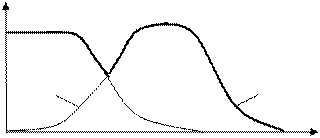
Рис.5. Операция объединения 3) Пересечение – это нечеткое множество с функцией принадлежности mАÇB(х)=min(mА(х), mВ(х)), " х Î Х.
mАÇB(х) х
Рис.6. Операция пересечения 4) Импликация – это нечеткое множество с функцией принадлежности mА® B(х)=max(1-mА(х), mВ(х)), " х Î Х. 5) Степень включения множества А в В – это величина n(А, В): n(А, В)=& (mА(х)® mB(х)).
n х
Рис.7. Степень включения Здесь результат операции &; понимается как минимум значений функции. В логике Заде: (mА(х)® mB(х)= (1-mА(х))Ú mB(х). n(А, В)=min (max(1-mА(х), mB(х)). В логике Лукасевича: mА(х)® mB(х)=1&(1-mА(х)+ mB(х)). Очевидно, если АÍ В, то n(А, В)=1, если АË В n(А, В)=0. 6) Степень равенства mА,B(х)=&(mА(х)«mВ(х))=&[ (mА(х)® mB(х))&(mB(х)® mA(х))], " х Î Х.
|

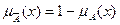


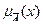
 m
m  mАÈB(х)
mАÈB(х) m
m  m
m 


