Определение ускорений
Ускорение точки А механизма определим по формуле:
Для определения ускорения точки В составим векторные уравнения:
Вектор
Выбираем масштаб mа плана ускорений и, согласно векторным уравнением (2), строим план ускорений:
где pа – отрезок, изображающий на плане ускорений вектор
Вектор
Для определения положения точки е на плане ускорений используем теорему подобия:
Аналогичным образом найдем на плане ускорений положение точек S1 и S2. Соединив полученные точки е, S1 и S2 с полюсом p получим векторы ускорений Для определения модулей ускорений точек измерим соответствующие отрезки на плане ускорений и умножим их на масштаб mа. Например: аВ =mа × pb = 1,33 × 76 = 101,08 м/с2. Результаты вычислений сводим а табл. 2. Таблица 2
Угловое ускорение звена 2 найдем по формуле:
Направление e2 соответствует направлению вектора
|

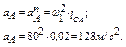
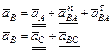 (2)
(2)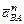 – нормальное ускорение точки В во вращательном движении звена АВ относительно точки А; модуль
– нормальное ускорение точки В во вращательном движении звена АВ относительно точки А; модуль 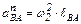 :
: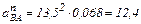 м/с2.
м/с2.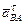 – касательное ускорение точки В в том же движении; модуль
– касательное ускорение точки В в том же движении; модуль  – ускорение точки С, равно 0.
– ускорение точки С, равно 0.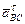 – ускорение точки В при поступательном движении звена 3 относительно направляющих; модуль аВС неизвестен, вектор аВС направлен горизонтально.
– ускорение точки В при поступательном движении звена 3 относительно направляющих; модуль аВС неизвестен, вектор аВС направлен горизонтально.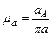 ,
,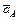 :
: (м/с2)/мм.
(м/с2)/мм.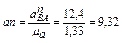 мм.
мм.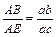 , откуда
, откуда 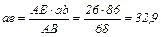 мм.
мм.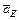 ,
, 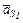 и
и 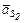 .
.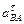
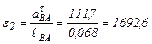 с-2.
с-2.


