Определение скоростей
Скорость точки А определим по формуле: uА = w1 × ℓОА, где w1 – угловая скорость звена 1; ℓОА – длина звена 1. uА = 80 × 0,02 = 1,6 м/с. Вектор Для определения скорости точки В составим векторные уравнения:
где uВА – скорость точки В во вращательном движении звена 2 относительно полюса А. Величина uВА неизвестна, вектор uC –скорость точки С равна 0, т. к. точка С принадлежит стойке. uВC –скорость точки В в относительном поступательном движении звена 3 относительно направляющих (стойки); модуль uВC неизвестен, а вектор Согласно векторным уравнениям (1) строим план скоростей: Определяем масштаб плана скоростей:
где pa – длина отрезка, изображающего на плане скоростей вектор скорости Для определения положения точки е на плане скоростей используем теорему подобия:
Строим точку е и соединяем ее с полюсом плана скоростей точкой Р. Вектор Аналогично находим положение точек S1 и S2 на плане скоростей. Для определения величины искомых скоростей, измерим соответствующие отрезки и умножим их на масштаб mu . Например: uВ = mu × рb = 0,02 × 48 = 0,96 м/с. Результат оформим в табл. 1. Таблица 1
Угловую скорость звена 2 находим по формулам:
где uВА – относительная скорость точки В во вращательном движении звена 2 относительно точки А. ℓАВ – длина звена.
Направление угловой скорости w2 находим, мысленно перенеся вектор
|

 направлен перпендикулярно звену 1 в сторону w1.
направлен перпендикулярно звену 1 в сторону w1.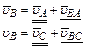 , (1)
, (1)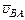 направлен перпендикулярно звену АВ.
направлен перпендикулярно звену АВ.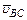 направлен горизонтально.
направлен горизонтально. (м/с) /мм,
(м/с) /мм,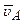
 , откуда имеем
, откуда имеем 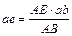 .
. мм.
мм. направлен из полюса Р к точке Е.
направлен из полюса Р к точке Е.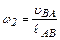 ,
, с-1.
с-1.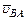 из плана скоростей в точку В механизма. Очевидно, что этот вектор стремится повернуть звено 2 относительно точки А по часовой стрелке. Это и есть направление w2.
из плана скоростей в точку В механизма. Очевидно, что этот вектор стремится повернуть звено 2 относительно точки А по часовой стрелке. Это и есть направление w2.


