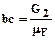Методические указания для заочников
по дисциплине: «Техническая механика»
2010 г. Введение Дисциплина «Техническая механика» состоит из трех частей:
По курсу «Техническая механика» студенты заочники должны выполнить контрольную работу, включающую в себя следующие задания: 1. Исследование плоского рычажного или шарнирного механизма 2. Расчет на прочность и жесткость типовых элементов: · расчет ступенчатого бруса · расчет вала · расчет на прочность балки 3. Расчет многоступенчатого привода. Задание на контрольную работу студент получает у преподавателя во время установочной лекции или в деканате (к.2.24 к. А) КТИ.
Общие методические указания Прежде чем приступить к выполнению контрольных заданий рекомендуется детально проработать необходимый теоретический материал по теме задания с кратким его конспективным изложением в тетради. Вопросы, предлагаемые к изучению, и список рекомендуемой литературы представлены ниже. Конспект предъявляется преподавателю на экзамене, а студент может пользоваться им на экзамене. После изучения теоретического материала необходимо разобрать решение задач, аналогичных тем, что включены в контрольную работу, и только после этого можно приступать к выполнению практических заданий. Примеры выполнения контрольных заданий приводятся ниже.
Требования, предъявляемые к выполнению контрольной работы. 1. Контрольная работа выполняется на листах формата А4 (стандартный лист писчей бумаги) чернилами аккуратно и разборчиво. 2. На листе выполняется рамка: отступ сверху, снизу и справа – 5 мм; слева – 20 мм. 3. Чертежи выполняются карандашом с использованием чертежных принадлежностей. 4. Графическая часть к заданию №1 (2 – я и 3 – я части задания) выполняется на формате А3. В правом нижнем углу приводится основная надпись (см. образец). 5. К каждому заданию обязательное наличие темы и условия. 6. Решения заданий должны содержать краткие пояснения и единицы измерений определяемых величин (см. примеры выполнения заданий). 7. Выполнение каждого задания начинать с новой страницы. 8. Страницы нумеруются в четкой последовательности, и в конце работы приводится содержание контрольной работы. 9. Обязательно наличие титульного листа; образец приведен ниже.
Внимание Контрольную работу необходимо представлять в деканат не позже чем за две недели до начала сессии!
Список литературы
Образец выполнения работы Исследование плоского шарнирного механизма
Исходные данные
q=10кг/м, положение кривошипа 11
1. Структурный анализ Исследуемый механизм состоит из одного неподвижного звена (стойки) и трех подвижных звеньев: ОА – кривошип, АЕ – шатун, ВС – коромысло. Звенья механизма образуют следующие кинематические пары: О (0-1); А (1-2); В (2-3); С (3-0). Все кинематические пары низшие, вращательные, пятого класса, одноподвижные. Степень подвижности механизма:
где: n – число подвижных звеньев, p5 – число кинематических пар пятого класса В нашем случае n=3, p5=4, следовательно:
Механизм имеет одну степень подвижности, т.е. для работы этого механизма одному из его звеньев – начальному звену необходимо задать одно независимое движение. Т.о. степень подвижности механизма определяет число его начальных звеньев. Исследуемый механизм образован присоединением к начальному механизму, который представляет собой начальное звено, связанное кинематической вращательной парой со стойкой, группы Асура II класса, II порядка, первого вида (рис. 2а и б).
2.Кинематический анализ механизма.
2.1. Построение кинематической схемы механизма для заданного положения начального звена. Выразим длину звеньев в м, определим масштаб длин ml и вычислим длину отрезков, изображающих звенья механизма на схеме. Результаты сведем в таблицу. Масштаб где ℓОА – длина звена ОА в м, ОА – отрезок в мм, изображающий на плане механизма звено 1.
Отрезок ВС, изображающий на схеме механизма звено 3
Аналогично найдем отрезки, изображающие на схеме другие звенья:
Строим кинематическую схему, соответствующую заданному положению кривошипа (№11).
2.2. Определение скоростей. Модуль скорости т. А найдем по формуле:
Для определения скорости т. В составим векторные уравнения:
где: VА – скорость точки А, модуль известен, а вектор VBA – относительная скорость точки В во вращательном движении звена 2 относительно полюса А, модуль ее известен, а вектор VС – скорость т. С, равная нулю, т. к. т. С принадлежит стойке. VBC – относительная скорость т. В во вращательном движении звена 3, относительно полюса С; модуль ее неизвестен, а вектор Решаем графически векторные уравнения (1), т. е. строим план скоростей. Масштаб плана скоростей
где: VА – скорость т. А в м/с pa – длина отрезка в мм, изображающего на плане скоростей вектор Положение точки е на плане скоростей найдем по теореме подобия:
Измерим полученные векторы на плане скоростей и умножим их на масштаб mv. В результате получим модули скоростей точек механизма. Например: Результаты измерений и вычислений сведем в таблицу:
Найдем угловые скорости звеньев 2 и 3.
Направление скорости w2 соответствует направлению относительной скорости VBA, т. е. направлению, в котором вектор
Направление w3 соответствует направлению движения часовой стрелки.
2.3. Определение ускорений. Модуль ускорения т. А найдем по формуле:
Для определения ускорения т. В, составим векторные уравнения:
где:
Вектор
Решаем графически векторные уравнения (2), т. е. строим план ускорений. Масштаб плана ускорений:
где аА – ускорение точки А. pа – длина отрезка, изображающего на плане ускорений вектор
Определим отрезки, изображающие на плане ускорений векторы
Положение точки е на плане ускорений найдем по теореме подобия.
Вектор Измерим длину векторов на плане ускорений и умножим их на масштаб mа. В результате получим модули ускорений. Например: Результаты измерений и вычислений сведем в таблицу:
Найдем угловые ускорения e2 и e3 звеньев 2 и 3.
Направление e2 соответствует направлению, в котором вектор
Т. о. звено ВС вращается равномерно.
3. Кинетостатический анализ механизма.
3.1 Определим силы, действующие на звенья механизма. Силы тяжести найдем по формуле:
где: m – масса звена q – ускорение свободного падения; примем q=10м/с2. G1=10×0.08×10=8н, G2=10×0.38×10=38н, G3=10×0.2×10=20н Силы тяжести приложены в центре масс звеньев и направлены вертикально вниз. Силы инерции найдем по формуле:
где m – масса звена, равная m=10ℓ. аS – ускорение центра масс звена, определены в п. 2.3 Fu2=3.8×10.46=39.7н, Fu3=2×4.98=9.96н Силы инерции приложены в центре масс звеньев и направлены противоположно ускорениям центра масс. Моменты сил инерции звеньев найдем по формуле:
где IS – момент инерции звена, равный IS=ℓ3 e - угловое ускорение звена Мu2=0.383×58.5=3.2кг/м2 Момент сил инерции звена направлен противоположно угловому ускорению звена. 3.2 Определяем реакции в кинематических парах механизма. Изобразим группу Асура (2 - 3) в масштабе 1:2 и покажем активные силы, действующие на ее звенья. Реакции, возникающие в кинематических парах А и С разложим на составляющие: Нормальные составляющие Касательные составляющие Результаты измерений сведем в таблицу.
Составим уравнение равновесия для звена 2:
Составим уравнение равновесия для звена 3 и найдем
Нормальные составляющие реакции
Определим масштаб плана сил:
где F21t - модуль силы в н ab – отрезок, изображающий вектор
Найдем длины отрезков, изображающих на плане сил векторы сил, известных по модулю: Например: Результаты вычислений сведем в таблицу.
Для определения реакции в кинематической паре В соединим точки e и k, т. е. замкнем силовой многоугольник построенный для сил, действующих на звено 2. В результате получим реакцию F23. Реакция F32 равна F23 по модулю, но противоположна ей по направлению. Для определения модулей искомых сил измерим длину соответствующих отрезков и умножим их на масштаб mF.
Бланки для выполнения работы в электронном виде (по желанию студента) Исследование плоского шарнирного механизма
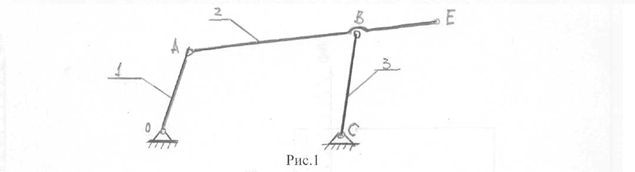
Рис.1 Исходные данные
q=10кг/м, положение кривошипа
1. Структурный анализ Исследуемый механизм состоит из одного неподвижного звена (стойки) и трех подвижных звеньев: ОА – кривошип, АЕ – шатун, ВС – коромысло. Звенья механизма образуют следующие кинематические пары: О (0-1); А (1-2); В (2-3); С (3-0). Все кинематические пары низшие, вращательные, пятого класса, одноподвижные. Степень подвижности механизма:
где: n – число подвижных звеньев, p5 – число кинематических пар пятого класса В нашем случае n=3, p5=4, следовательно:
Механизм имеет одну степень подвижности, т.е. для работы этого механизма одному из его звеньев – начальному звену необходимо задать одно независимое движение. Т.о. степень подвижности механизма определяет число его начальных звеньев. Исследуемый механизм образован присоединением к начальному механизму, который представляет собой начальное звено, связанное кинематической вращательной парой со стойкой, группы Асура II класса, II порядка, первого вида (рис. 2а и б).
Рис.2 Следовательно, данный механизм является механизмом II класса.
2.Кинематический анализ механизма.
2.1. Построение кинематической схемы механизма для заданного положения начального звена. Выразим длину звеньев в м, определим масштаб длин ml и вычислим длину отрезков, изображающих звенья механизма на схеме. Результаты сведем в таблицу. Масштаб где ℓОА – длина звена ОА в м, ОА – отрезок в мм, изображающий на плане механизма звено 1.
Отрезок ВС, изображающий на схеме механизма звено 3
Аналогично найдем отрезки, изображающие на схеме другие звенья:
Строим кинематическую схему, соответствующую заданному положению кривошипа
2.2. Определение скоростей. Модуль скорости т. А найдем по формуле:
Для определения скорости т. В составим векторные уравнения:
где: VА – скорость точки А, модуль известен, а вектор VBA – относительная скорость точки В во вращательном движении звена 2 относительно полюса А, модуль ее известен, а вектор VС – скорость т. С, равная нулю, т. к. т. С принадлежит стойке. VBC – относительная скорость т. В во вращательном движении звена 3, относительно полюса С; модуль ее неизвестен, а вектор Решаем графически векторные уравнения (1), т. е. строим план скоростей. Масштаб плана скоростей
где: VА – скорость т. А в м/с pa – длина отрезка в мм, изображающего на плане скоростей вектор Положение точки е на плане скоростей найдем по теореме подобия:
Измерим полученные векторы на плане скоростей и умножим их на масштаб mv. В результате получим модули скоростей точек механизма. Например: Результаты измерений и вычислений сведем в таблицу:
Найдем угловые скорости звеньев 2 и 3.
Направление скорости w2 соответствует направлению относительной скорости VBA, т. е. направлению, в котором вектор
Направление w3 соответствует направлению движения часовой стрелки.
2.3. Определение ускорений. Модуль ускорения т. А найдем по формуле:
Для определения ускорения т. В, составим векторные уравнения:
где:
Вектор
Решаем графически векторные уравнения (2), т. е. строим план ускорений. Масштаб плана ускорений:
где аА – ускорение точки А. pа – длина отрезка, изображающего на плане ускорений вектор
Определим отрезки, изображающие на плане ускорений векторы
Положение точки е на плане ускорений найдем по теореме подобия.
Вектор Измерим длину векторов на плане ускорений и умножим их на масштаб mа. В результате получим модули ускорений. Например: Результаты измерений и вычислений сведем в таблицу:
Найдем угловые ускорения e2 и e3 звеньев 2 и 3.
Направление e2 соответствует направлению, в котором вектор
Т. о. звено ВС вращается равномерно.
3. Кинетостатический анализ механизма.
3.1 Определим силы, действующие на звенья механизма. Силы тяжести найдем по формуле:
где: m – масса звена q – ускорение свободного падения; примем q=10м/с2. Силы тяжести приложены в центре масс звеньев и направлены вертикально вниз.. Силы инерции найдем по формуле:
где m – масса звена, равная m=10ℓ. аS – ускорение центра масс звена, определены в п. 2.3 Силы инерции приложены в центре масс звеньев и направлены противоположно ускорениям центра масс. Моменты сил инерции звеньев найдем по формуле:
где IS – момент инерции звена, равный IS=ℓ3 e - угловое ускорение звена Момент сил инерции звена направлен противоположно угловому ускорению звена. 3.2 Определяем реакции в кинематических парах механизма. Изобразим группу Асура (2 - 3) в масштабе 1:2 и покажем активные силы, действующие на ее звенья. Реакции, возникающие в кинематических парах А и С разложим на составляющие: Нормальные составляющие Касательные составляющие Результаты измерений сведем в таблицу.
Составим уравнение равновесия для звена 2:
Составим уравнение равновесия для звена 3 и найдем
Нормальные составляющие реакции
Определим масштаб плана сил:
где F21t - модуль силы в н ab – отрезок, изображающий вектор Найдем длины отрезков, изображающих на плане сил векторы сил, известных по модулю: Например: Результаты вычислений сведем в таблицу.
Для определения реакции в кинематической паре В соединим точки e и k, т. е. замкнем силовой многоугольник построенный для сил, действующих на звено 2. В результате получим реакцию F23. Реакция F32 равна F23 по модулю, но противоположна ей по направлению. Для определения модулей искомых сил измерим длину соответствующих отрезков и умножим их на масштаб mF.
|

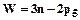 ,
,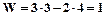

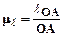 ,
,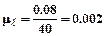 м/мм
м/мм мм.
мм.
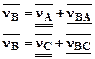 (1)
(1) направлен перпендикулярно звену ОА в сторону w1.
направлен перпендикулярно звену ОА в сторону w1.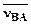 направлен перпендикулярно звену АВ.
направлен перпендикулярно звену АВ. направлен перпендикулярно звену ВС.
направлен перпендикулярно звену ВС. ,
,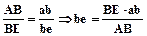 ;
; 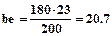 мм
мм м/с.
м/с.
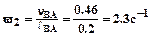
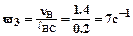
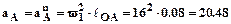 м/с2
м/с2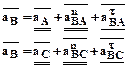 (2).
(2).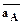 - ускорение точки А, известное по модулю; вектор
- ускорение точки А, известное по модулю; вектор  - нормальное относительное ускорение т. В во вращательном движении звена 2 относительно полюса А. Модуль
- нормальное относительное ускорение т. В во вращательном движении звена 2 относительно полюса А. Модуль 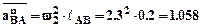 м/с2.
м/с2. - касательное ускорение т. В во вращении звена АВ относительно полюса А; модуль
- касательное ускорение т. В во вращении звена АВ относительно полюса А; модуль  - ускорение т. С, равное 0, т. к. точка С принадлежит стойке.
- ускорение т. С, равное 0, т. к. точка С принадлежит стойке. - нормальное ускорение т. В во вращении звена ВС относительно полюса С. Модуль
- нормальное ускорение т. В во вращении звена ВС относительно полюса С. Модуль  м/с2, вектор
м/с2, вектор 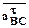 - касательное ускорение т. В во вращении звена ВС относительно полюса С. Модуль
- касательное ускорение т. В во вращении звена ВС относительно полюса С. Модуль  ,
,
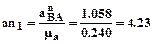 мм
мм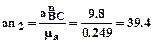 мм.
мм. , откуда следует, что
, откуда следует, что 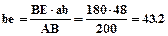 мм.
мм.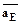 получим, соединив полюс p с точкой е.
получим, соединив полюс p с точкой е.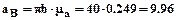 м/с2.
м/с2.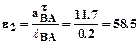 с-2.
с-2. .
.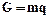 ,
, ,
,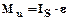 ,
,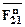 и
и 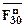 направлены вдоль соответствующих звеньев; касательные составляющие
направлены вдоль соответствующих звеньев; касательные составляющие  и
и 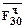 направлены перпендикулярно звеньям.
направлены перпендикулярно звеньям. .
. 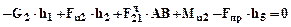
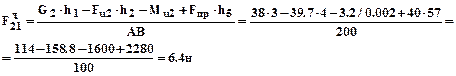
 :
:


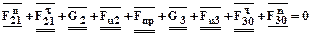
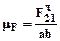 ,
,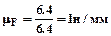


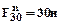
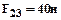
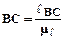 мм.
мм.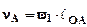

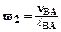



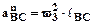 вектор
вектор 



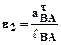
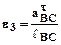 .
. ,
,