Решение. Определим масштаб длин, для чего примем длину отрезка ОА, изображающего на чертеже кривошип, равным 40 мм
Определим масштаб длин, для чего примем длину отрезка ОА, изображающего на чертеже кривошип, равным 40 мм. Тогда масштабный коэффициент будет равен:
Определим отрезки, изображающие на чертеже остальные звенья в выбранном масштабе:
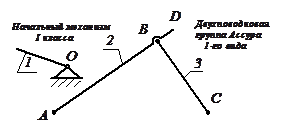
Вычерчиваем схему механизма в соответствии с выбранным масштабом для заданного узла положении кривошипа. Механизм состоит из одного неподвижного звена – стойки – и трех подвижных звеньев n = 3. Звенья механизма образуют между собой низшие одноподвижные вращательные пары пятого класса: кинематическая пара О образована стойкой и кривошипом; кинематическая пара А образована звеньями и 1 и 2; кинематическая пара В образована звеньями и кинематическая пара С образована звеньями 3 и стойкой. Таким образом, в составе механизма четыре кинематических пары пятого класса: р5 = 4. Число степеней свободы механизма определим по формуле Чебышева: W = 3 × n – 2 ×р5 – р4, где W – число степеней свободы механизма; n – число подвижных звеньев; р5 – число кинематических пар пятого класса; р4 – число кинематических пар четвертого класса. W = 3 × 3 – 3 × 4 = 1. Таким образом, механизм имеет одну степень подвижности. Это означает, что в рассматриваемом механизме достаточно задать закон движения только одному звену (в данном случае звену 1, которое является ведущим), чтобы закон движения всех остальных звеньев был бы определенным. Для определения класса механизма разложим его на группы Асура.
Таким образом, в состав механизма входит только одна группа Ассура, то класс и порядок механизма соответственно классу и порядку этой группы Ассура. Следовательно, наш механизм является механизмом II второго класса второго порядка. 1. Определение линейных скоростей точек звеньев механизма. Скорость точки А определим по формуле: uА = w1 × ℓОА, где w1 – угловая скорость звена 1; ℓОА – длина звена 1. uА = 12 × 0,05 = 0,6 м/с. Так как точка А относительно точки О совершает вращательное движение, то вектор Для определения скорости точки В составим систему двух векторных уравнений, которые связывают искомую скорость с другими скоростями. Это возможно сделать, так как точка В принадлежит одновременно двум звеньям – 2 и 3. Первое векторное уравнение составим, считая, что точка принадлежит звену 2, а вторая – что звену 3.
где
Сведем систему к одному уравнению и подчеркнем двумя чертами векторы, известные и по величине и направлению и одной чертой векторы, направление которых известно, но неизвестен модуль. В результате имеем одно векторное уравнение с двумя неизвестными:
Решим его графически, т. е. построим план скоростей. Для этого выбираем на плоскости произвольную точку р – полюс плана, скоростей, которая является началом отсчета, и откладываем от нее отрезок Примем длину отрезка
и покажет, сколько метров в секунду действительной величины скорости содержится в одном миллиметре отрезка на чертеже. В соответствии с правой частью уравнения на плане скоростей через точку а проводим прямую, перпендикулярную к звену 2 механизма (это направление вектора
|

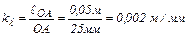 .
.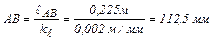 .
.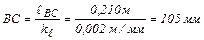 .
.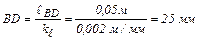 .
.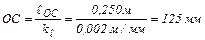 .
.
 направлен перпендикулярно звену ОА.
направлен перпендикулярно звену ОА.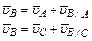 ,
,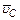 – вектор абсолютной скорости точки С, равный нулю, так как точка принадлежит одновременно и стойке.
– вектор абсолютной скорости точки С, равный нулю, так как точка принадлежит одновременно и стойке. – вектор относительной скорости во вращении звена АВ вокруг точки А направлен перпендикулярно этому звену, по модулю неизвестен.
– вектор относительной скорости во вращении звена АВ вокруг точки А направлен перпендикулярно этому звену, по модулю неизвестен.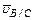 – вектор относительной скорости АО вращении звена ВС относительно точки С направлен перпендикулярно звена ВС, модуль неизвестен.
– вектор относительной скорости АО вращении звена ВС относительно точки С направлен перпендикулярно звена ВС, модуль неизвестен. .
.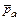 , перпендикулярный звену ОА в направлении движения точки А.
, перпендикулярный звену ОА в направлении движения точки А.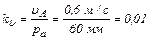 м/с×мм,
м/с×мм,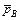 , изображающего на плане
, изображающего на плане
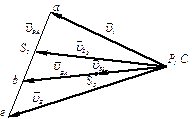
 План ускорений mа = 0,667 м×мм/с2
План ускорений mа = 0,667 м×мм/с2



