Способ равноточных допусков
При решении задач этим способом условно принимают, что возрастание допуска линейных размеров при возрастании номи-нального размера имеет место ту же закономерность, что и воз-растание допуска диаметра. Эта закономерность выражена фор-мулой для единицы допуска i. Для 5-17 квалитетов
где D – в мм, i - в мкм. Количество единиц допуска i в допусках 5-13-го квалитетов, т.е. величина Таблица 5.1 - Формула допусков квалитетов от 5 до 15
Исходя из табл. 5.1 в общем виде формула допуска имеет вид
где Значения i для основных интервалов в диапазоне до 315 мм приведены в табл. 5.2. Таблица 5.2 - Значения i для основных интервалов
Выразив допуски всех составляющих в единицах допус-ка, получаем по (3.3)
Полагая, что все размеры равноточны, т.е. должны выполня- ться по одному квалитету, следует принять, что
где
Величины, стоящие в знаменателе, выбирают из табл. 5.2, ве-личина Полученное значение Допустимо, чтобы Пример 3. В редукторе (рис. 2.2) величина зазора Решение. Это задача второго типа. Замыкающее звено S. Решение удобнее расположить в виде таблицы (см. табл. 5.3). Схему цепи можно не составлять, т.к. она показана на эскизе. Определяя
Значение В графе 3 показаны допуски 9-го квалитета на диаметры соот-ветствующего номинального размера (см. ГОСТ 25346, приложе-ние Б). Сумма допусков меньше допуска замыкающего звена на 27 мкм. Чтобы уравнение (3.3) удовлетворялось, уменьшим до-пуск Таблица 5.3 – К решению примера 3
Определим номинальный размер и предельные отклонения замыкающего звена Размер
Предельные размеры зазора:
Следовательно, предельные отклонения
Назначим отклонения всех составляющих, кроме размера 200 в «минус», так как все размеры являются охватываемыми, а раз-мер 200 мм может иметь отклонения любого знака. Отклонения
Проверяем:
т.е. допуск замыкающего размера равен сумме допусков состав-ляющих размеров.
|

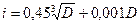 ,
, приведены в табл. 5.1.
приведены в табл. 5.1.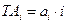 , (5.2)
, (5.2)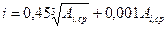 . (5.3)
. (5.3)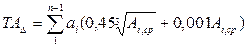 .
. ,
, - количество единиц допуска или коэффициент точности данной размерной цепи. Вынося
- количество единиц допуска или коэффициент точности данной размерной цепи. Вынося  , откуда
, откуда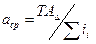 . (5.4)
. (5.4)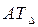 по условиям задачи задана. Величина
по условиям задачи задана. Величина 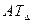 превышало
превышало 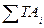 на 5-6%, если не-обходимо назначить допуски, взятые из стандарта, и не изменять их так, чтобы уравнение (3.3) удовлетворялось тождественно.
на 5-6%, если не-обходимо назначить допуски, взятые из стандарта, и не изменять их так, чтобы уравнение (3.3) удовлетворялось тождественно.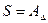 должна быть в пределах 1,0-1,4 мм. Требуется назначить допуски и предельные отклонения на составляющие размеры для условия обеспечения полной взаимозаменяемости, если
должна быть в пределах 1,0-1,4 мм. Требуется назначить допуски и предельные отклонения на составляющие размеры для условия обеспечения полной взаимозаменяемости, если 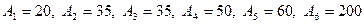 .
.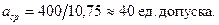
 . Принятые размеры приведены в графе 4.
. Принятые размеры приведены в графе 4. , мм
, мм
 , мкм
, мкм
 , мм (принятое)
, мм (принятое)

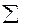
 , а затем назначим отклонения сос-тавляющих размеров.
, а затем назначим отклонения сос-тавляющих размеров. - увеличивающее звено, остальные звенья умень-шающие. По уравнению (2.1)
- увеличивающее звено, остальные звенья умень-шающие. По уравнению (2.1)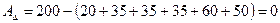 .
.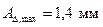
 и
и 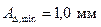 .
.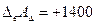 ;
; 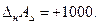
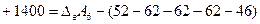 ;
; 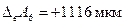 ;
;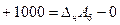 ;
;  .
. и
и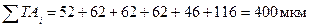 ,
,


