Расчет размерных цепей методом полной взаимозаменяемости
Решить размерную цепь – значит найти такие предельные значения ее увеличивающих и уменьшающих размеров, при кото-рых предельные размеры замыкающего звена отвечали бы требо-ваниям конструкции или технологии. Обычно расчет допусков в размерных цепях сводится к решению одной из следующих задач. Тип первый (прямая задача) – определить допуск и отклоне-ния замыкающего размера, если известны допуски и отклонения уменьшающих и увеличивающих размеров размерной цепи. Тип второй (обратная задача) – определить наиболее рацио-нальные допуски и отклонения увеличивающих и уменьшающих размеров, если известны допуск и отклонения замыкающего размера. Существует два метода решения размерных цепей: метод полной взаимозаменяемости и метод неполной взаимозаменяе-мости. Ниже будет рассмотрен только метод полной взаимозаменяе-мости. Этот метод решения размерных цепей сводится к так на-зываемому расчету на максимум и минимум. Учитывая уравнение (2.1), получаем для предельных разме-ров цепи соотношения:
т.е. максимальное значение замыкающего размера ( Вычитая почленно из уравнений (3.1) уравнение (2.1) полу-чим уравнение, связывающие предельные отклонения:
Из полученных уравнений можно сделать выводы: 1) Верхнее отклонение замыкающего размера ( 2) Нижнее отклонение замыкающего размера ( Вычитая почленно нижние уравнения из верхних в уравне-ниях (3.1) или (3.2) получаем уравнение, связывающее допуски в размерной цепи:
т.е. допуск замыкающего размера (
|
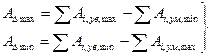, (3.1)
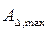) рав-но разности между суммой наибольших значений увеличиваю-щих размеров (
) и суммой наименьших значений умень-шающих размеров (
). Минимальное значение замыкаю-щего размера (
) равно разности между суммой наимень-ших значений увеличивающих размеров (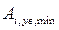
) и суммой наибольших значений уменьшающих размеров (
).
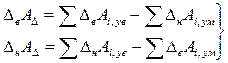(3.2)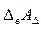
) равно разности между суммой верхних предельных отклонений увеличивающих размеров (
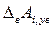) и суммой нижних пре-дельных отклонений уменьшающих размеров (
).
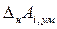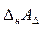) равно разности между суммой нижних предельных отклонений увеличивающих размеров (
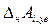) и суммой верхних пре-дельных отклонений уменьшающих размеров (
).
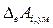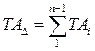, (3.3)
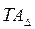) равен сумме допусков всех размеров, входящих в размерную цепь. Отсюда вытекает следующее правило, что при заданном допуске на замыкающий размер, нужно стремиться к тому, чтобы количество звеньев в размерной цепи было наименьшим.
