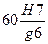Способ равных допусков
В том случае, когда все размеры цепи входит в один интервал диаметров, можно назначить равные допуски на все составляю-щие, т.е. принять
Уравнение (2.3) примет вид
где n – число звеньев цепи, включающее замыкающее. Если для k составляющих допуски назначены и сумма этих допусков равна f, то формула (5.1) примет вид
Пример 2. Простейшей сборочной размерной цепью является трехзвенная цепь размеров цилиндрического сопряжения, т.е. отверстия D, вала d и зазора S. Замыкающий размер – зазор
Рисунок 5.1 – К примеру 2 расчета размерных цепей Решение. Так как несоосность равна половине зазора (рис. 5.2), то наибольший зазор равен удвоенной несоосности
Рисунок 5.2 – Соотношение между величиной зазора Номинальные размеры отверстия и вала одинаковы, следова-тельно, можно применить способ равных допусков. По формуле (5.1) получаем для
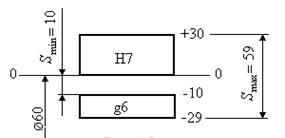
Допуск 25 мкм для диаметра 60 (ГОСТ 25346, см. приложе-ние Б) не предусмотрен. Для размера 60 по 6-му квалитету до-пуск равен 19 мкм, а по - квалитету – 30 мкм. Так как обычно применяют сопряжения отверстий 7-го квалитета с валами 6-го квалитета (см. приложение Д), то приняв ТА 1=30 мкм,а Для окончательного решения следует подобрать наиболее подходящую посадку. По ГОСТ 25346 (см. приложения В, Г) находим, что верхнее отклонение вала g6 равно минус 10, а ниж-нее отклонение отверстия Н7 равно нулю, следовательно такой посадкой является Ø
Рисунок 5.3 – Схема поля допуска посадки Ø
|

 .
.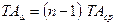 , откуда
, откуда 
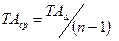 , (5.1)
, (5.1)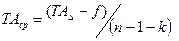 . (5.1, a)
. (5.1, a)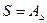 , диаметр отверстия
, диаметр отверстия 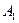 - увеличивающий размер, диаметр вала – уменьшающий размер (рис. 5.1). Расчет (по гидродинами-ческой теории смазки) подвижной посадки показывает, что в со-пряжении Ø60 наименьший зазор должен быть равен
- увеличивающий размер, диаметр вала – уменьшающий размер (рис. 5.1). Расчет (по гидродинами-ческой теории смазки) подвижной посадки показывает, что в со-пряжении Ø60 наименьший зазор должен быть равен 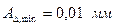 . Допустимая несоосность не должна превы-шать 0,03 мм.
. Допустимая несоосность не должна превы-шать 0,03 мм.
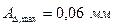 , тогда
, тогда 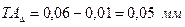 .
.
 и несоосностью
и несоосностью 
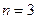
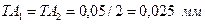 .
.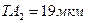 , получим
, получим  . Что удовлетво-ряет условию примера.
. Что удовлетво-ряет условию примера.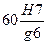 (рис. 5.3).
(рис. 5.3).