Основные теоретические положения. Индуктивная катушка и конденсатор относятся к реактивным элементам
Индуктивная катушка и конденсатор относятся к реактивным элементам. Протекающий по ним переменный ток вызывает возникновение магнитного или электрического полей соответственно, что сопровождается обратимыми преобразованиями электрической энергии в энергию магнитного или электрического полей. Энергия электрической цепи, вовлечённая в этот процесс, называется реактивной. Реактивная энергия циркулирует между реактивным элементом и источником. В этом заключается основное отличие реактивных элементов от активного (резистора), на котором происходит необратимый процесс преобразования электрической энергии в тепловую, рассеиваемую в окружающей среде. Энергия электрической цепи, участвующая в данном процессе, называется активной. При этом на реактивных элементах наблюдается фазовый сдвиг между синусоидами тока и напряжения, в то время как на активном элементе угол между током и напряжением равен нулю. В настоящей работе исследуются индуктивная катушка с постоянными параметрами R, L (рис. 4.1) и конденсатор переменной ёмкости C (рис. 4.2). Индуктивная катушка представляет собой проводник, намотанный на сердечник. Сердечники обычно выполняются в виде стержня или тора из специальных материалов, предназначенных для концентрации в себе магнитного потока, возникающего при протекании тока по виткам проводника.
В связи со своим конструктивным исполнением индуктивная катушка характеризуется двумя параметрами: а) активным сопротивлением R, представляющим собой активное сопротивление проводника, из которого выполняются витки, б) индуктивностью L, характеризующей основное свойство катушки – создание магнитного поля. В результате этого индуктивная катушка представляется в виде схемы замещения, состоящей из последовательного соединения идеального резистивного элемента с сопротивлением R, равным активному сопротивлению проводника катушки, и идеального индуктивного элемента с индуктивностью L, равной индуктивности катушки (рис. 4.1). Полное сопротивление катушки записывается через ток и напряжение на ней по закону Ома:
где: Uк и I – действующие значения напряжения и тока катушки (под действующим значением тока понимают значение периодического тока, равное такому значению постоянного тока, который за время одного периода производит тот же самый тепловой или электродинамический эффект, что и периодический ток). На схеме замещения катушка рассматривается как последовательное соединение R и L элементов, поэтому общее сопротивление катушки должно являться суммой сопротивлений этих элементов. Однако, поскольку сопротивления R и L элементов обусловлены различными факторами (электрическим сопротивлением металла и ЭДС самоиндукции соответственно), вводят понятие комплексного сопротивления
где: R, В связи с вышесказанным, полное сопротивление катушки представляется как гипотенуза прямоугольного треугольника сопротивлений (рис. 4.3), один катет, которого равен R, а другой – XL. Из треугольника сопротивлений вытекают следующие зависимости:
Напряжение на катушке (рис. 4.1), находится (аналогично полному сопротивлению) векторной суммой напряжений последовательно соединённых элементов:
Вектор полного напряжения на индуктивной катушке Векторы напряжений
Полная мощность катушки Sк по определению равна произведению тока катушки I и напряжения на катушке Uк, т. е.
Полная мощность Sк связана с активной Р и реактивной QL мощностями индуктивной катушки выражением
Активная мощность P численно равна электрической энергии, преобразующейся на катушке в теплоту за единицу времени, и определяется как
Реактивная мощность QL численно равна мгновенной мощности, находящейся в процессе обмена между магнитным полем катушки и источником электрической энергии. Величина реактивной мощности определяется формулами
Графически связь между Sк, P и QL можно представить в виде прямоугольного треугольника мощностей (рис. 4.5), гипотенуза которого равна Sк, а катеты – P и QL. Треугольник мощностей подобен треугольникам сопротивлений и напряжений. Из него вытекают следующие соотношения:
Величина соs(φ) называется коэффициентом мощности. Данный коэффициент показывает какую часть от полной мощности S составляет активная мощность P (из треугольника мощностей
Конденсатор представляет собой обкладки, разделённые диэлектриком. Данная конструкция способствует возникновению электрического поля между обкладками, на которых скапливаются разноимённые электрические заряды. В любом диэлектрике, разделяющем заряженные обкладки конденсатора, будут возникать токи утечки за счёт проникновения зарядов сквозь него. Однако данные токи утечки настолько малы, что ими обычно пренебрегают и тогда на схеме замещения (рис. 4.2) конденсатор представляется в виде идеального ёмкостного элемента с ёмкостью C (при учёте токов утечки схема замещения изображается в виде параллельно соединённых идеальных резистивного и ёмкостного элементов). В результате, полное сопротивление конденсатора Zконд. принимается равным его ёмкостному сопротивлению XC:
где: UС и I – действующие значения напряжения и тока конденсатора. Ёмкостное сопротивление связано с ёмкостью C следующим образом:
В связи с тем, что полное сопротивление конденсатора принимается без активной составляющей, на ёмкостном элементе работа не совершается, т. е. активная мощность Р конденсатора равна нулю. Однако в цепи с ёмкостным элементом происходит периодический обмен энергией между источником и электрическим полем данного элемента. Интенсивность такого обмена характеризуют реактивной мощностью:
Полная мощность конденсатора равна его реактивной мощности.
|


 ,
,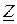 (представляют общее сопротивление R и L элементов в виде комплексного числа) и рассматривают активное сопротивление R в качестве вещественной части данного комплексного сопротивления, а индуктивное сопротивление XL, вызываемое индуктивностью L, – в качестве мнимой части:
(представляют общее сопротивление R и L элементов в виде комплексного числа) и рассматривают активное сопротивление R в качестве вещественной части данного комплексного сопротивления, а индуктивное сопротивление XL, вызываемое индуктивностью L, – в качестве мнимой части:  . Благодаря этому R и XL откладываются по различным осям на комплексной плоскости и поэтому не складываются в одно целое подобно скалярным величинам, а их сумма находится как модуль комплексного числа, т. е. как векторная сумма. Таким образом, полное сопротивление индуктивной катушки связано с параметрами её схемы замещения следующим образом:
. Благодаря этому R и XL откладываются по различным осям на комплексной плоскости и поэтому не складываются в одно целое подобно скалярным величинам, а их сумма находится как модуль комплексного числа, т. е. как векторная сумма. Таким образом, полное сопротивление индуктивной катушки связано с параметрами её схемы замещения следующим образом: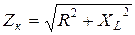 ,
,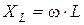 – активная и индуктивная составляющие сопротивления соответственно, ω=2∙π· f – угловая частота тока, f – частота тока в цепи.
– активная и индуктивная составляющие сопротивления соответственно, ω=2∙π· f – угловая частота тока, f – частота тока в цепи.
 . Вектор
. Вектор  активной составляющей полного напряжения катушки совпадает по направлению с вектором тока
активной составляющей полного напряжения катушки совпадает по направлению с вектором тока 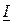 , а вектор
, а вектор  реактивной составляющей – опережает вектор тока
реактивной составляющей – опережает вектор тока  . Действующие значения напряжений Uк, UR, UL, тока I и соответствующие сопротивления катушки связаны следующими зависимостями:
. Действующие значения напряжений Uк, UR, UL, тока I и соответствующие сопротивления катушки связаны следующими зависимостями: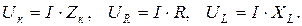
 опережает вектор тока
опережает вектор тока 
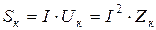 .
. .
. .
. .
.
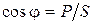 ).
).
 ,
,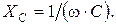
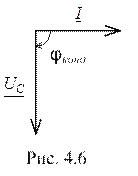 Векторная диаграмма тока и напряжения на конденсаторе приведена на рисунке 4.6. Вектор
Векторная диаграмма тока и напряжения на конденсаторе приведена на рисунке 4.6. Вектор  напряжения на конденсаторе отстаёт от вектора тока
напряжения на конденсаторе отстаёт от вектора тока  .
.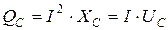 .
.


