Расчетные соотношения для исследуемых электрических цепей. Исследование электрических цепей синусоидального тока
Лабораторная работа № 2 Исследование электрических цепей синусоидального тока Цель работы Исследование соотношения для тока и напряжений электрических цепей синусоидального тока при последовательном соединении участков с катушкой индуктивности и емкостью.
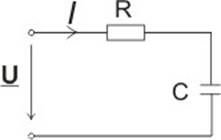
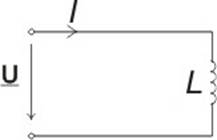
Пояснения к лабораторному стенду Схемы исследуемых электрических цепей приведены на рис. 1 – 4
Рис. 1 Рис. 2
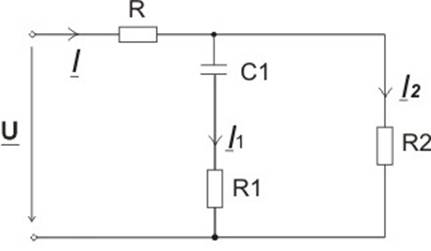
Рис. 3
Рис. 4
Для сборки схемы используются элементы универсального лабораторного стенда. Измерение действующих значений напряжений в схемах осуществляется с помощью цифрового вольтметра, измерение углов сдвига фаз между напряжениями и токами – с помощью фазометра.
Расчетные соотношения для исследуемых электрических цепей В однофазных электрических цепях в большинстве случаев действуют ЭДС, изменяющиеся по синусоидальному закону
где e – мгновенное значение ЭДС; Em – амплитудное значение;
f – частота; y e – начальная фаза. Токи и напряжения в таких цепях синусоидальны:
Фазовый сдвиг между напряжением и током
Наряду с мгновенным и амплитудным используется понятие о среднеквадратичном (действующем) значении переменного тока, напряжения, ЭДС.
Действующее значение синусоидального тока
В большинстве случаев расчета цепей синусоидального тока производят комплексным методом, который позволяет осуществить переход от тригонометрических уравнений к алгебраическим, составленным относительно комплексов тока и напряжения. Известно, что синусоидально изменяющаяся величина может быть условно (символически) прeдставлена в виде комплексного числа A. Это лежит в основе замены синусоидальных функций вращающимися векторами. Так, например, проекция вектора

Рис. 5
Совокупность векторов, изображающих синусоидально изменяющиеся токи, напряжения, ЭДС некоторой электрической цепи, называется векторной диаграммой. Векторные диаграммы строятся для момента времени t = 0. Комплексные сопротивления индуктивности и емкости соответственно можно найти как
Зная комплексные сопротивления можно определить величины индуктивности и емкости элементов
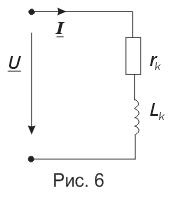
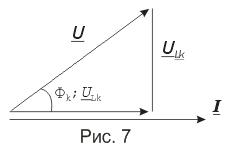
Реальная катушка индуктивности обладает существенным электрическим сопротивлением и может быть представлена эквивалентной схемой, состоящей из последовательно включенных индуктивности L K и активного сопротивления r K (рис. 6). Векторная диаграмма для такой катушки приведена на рис 7.
Ток в одноконтурной цепи, состоящей из последовательно соединенных элементов, находится по закону Ома.
где Z – входное комплексное сопротивление цепи, равно сумме сопротивлений отдельных ее элементов:
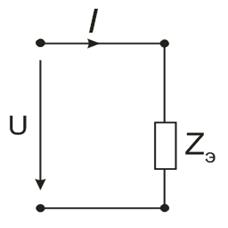
При расчете сложной разветвленной цепи с одним источником электрической энергии чаще всего применяют метод преобразования. Он состоит в приведении исходной схемы (например, рис. 3,4) к простейшей, содержащей одно эквивалентное сопротивление Z э. Преобразование исходной схемы заключается в определении отдельных эквивалентных сопротивлений при последовательном и параллельном соединении. Ток I в преобразованной цепи (являющийся, одновременно и входным током исходной схемы) находится также по закону Ома. Рассмотрим для примера расчет токов в схеме рис. 3. Комплексные сопротивления отдельных ветвей схем (рис. 8) определяются как
Рис. 8 Рис. 9
Определим эквивалентное комплексное сопротивление параллельных ветвей.
Входное (эквивалентное) сопротивление всей цепи (рис.9)
По закону Ома находим входной ток, принимая начальную фазу входного напряжения b = 0:
Найдем напряжение на параллельных ветвях
Тогда
Зная токи в ветвях, можно определить напряжения на отдельных параметрах катушки
|


 ,
,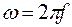 – угловая частота;
– угловая частота;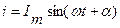 ;
; .
.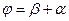 .
. .
.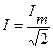 .
.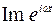 на минимальную ось для момента времени t показана на рис. 5.
на минимальную ось для момента времени t показана на рис. 5. ;
; 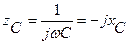 .
.
 .
.
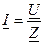 ,
,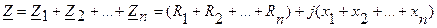 .
.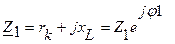 ;
; .
.
 .
.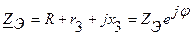 .
. .
.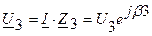 .
. ;
;  ;
;  .
.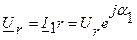 ;
;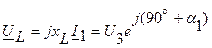 .
.


