Понятие о нечетких множествах
В 1965 г. появилась статья Л. Заде «Fuzzy Sets», которая положила начало теории нечетких множеств (НМ).Основная идея Заде: человеческий способ рассуждений, опирающийся на естественные языки, не может быть описан в рамках традиционных формализмов. Программа Заде состояла в построении новой математической дисциплины, в основе которой лежала бы не классическая теория множеств (чётких множеств), а теория НМ. Тогда можно построить нечеткие аналоги всех основных математических понятий и создать необходимый формальный аппарат для моделирования человеческих рассуждений и человеческого способа решения задач. Выделяют два основных подхода к формализации нечеткости. 1. Подход. НМ образуется путем введения обобщенного понятия принадлежности, т.е. расширения множества (0, 1) значений характеристической функции до континуума [0, 1]. Это означает, что переход от полной принадлежности объекта классу (множеству) к полной его непринадлежности происходит не скачком, а плавно, постепенно, причём принадлежность элемента множеству выражается числом из интервала [0, 1]. Таким образом, НМ можно записать в виде
Существует множество операций над НМ, часть которых аналогичны операциям над четкими множествами. Как правило, они описываются через функции принадлежности. Например,
В НМ сохраняются известные свойства операций (рефлексивность, транзитивность и т.д.) и законы (идемпотентности, коммутативности, двойного отрицания, закон де Моргана). Однако для НМ не выполняется закон комплементарности (закон исключения третьего), т.е. справедливы соотношения
Рассматривают следующие виды НМ: Нормальные НМ, если Субнормальные НМ, если НМ уровня a (НМА): Чёткое множество А *, ближайшее к НМ, определяется как
Нечеткая функция – отображение 2. Подход. Всякое НМ можно разложить по множествам уровня (теорема декомпозиции):
То есть нечеткость выражается с помощью набора иерархически упорядоченных чётких множеств. Следовательно, для конечного числа n градаций рассматриваемого свойства n –нечёткое множество задается через n –ку обычных множеств Для бесконечного числа градаций имеем бесконечное семейство множеств Тогда размытость моделируется отображением М из класса функций
а) М (0)= Х; б) и соответствующими операциями над ними. Связь между первым и вторым представлениями НМ устанавливается теоремой представления, согласно которой классы F (X) (класс функций первого представления) и
|

 , где
, где  – функция принадлежности.
– функция принадлежности.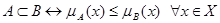 отношение вложения;
отношение вложения; дополнение,
дополнение,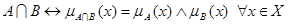 произведение,
произведение, сумма.
сумма. .
. .
.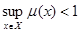 .
. , т.е. НМА – четкое подмножество универсального множества Х (
, т.е. НМА – четкое подмножество универсального множества Х ( ). Множество строгого уровня:
). Множество строгого уровня: 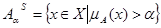 . Носителем НМА является множество Х, для элементов которого
. Носителем НМА является множество Х, для элементов которого  .
.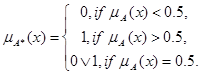
 , которое каждому
, которое каждому 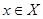 ставит в соответствие
ставит в соответствие 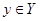 со степенью
со степенью 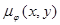 . При этом может быть или нечеткое Х или нечеткое Y. Нечеткая функция определяет нечёткую поверхность принадлежности в X*Y (X, Y – произвольные множества).
. При этом может быть или нечеткое Х или нечеткое Y. Нечеткая функция определяет нечёткую поверхность принадлежности в X*Y (X, Y – произвольные множества).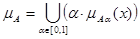 , где
, где 
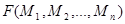 , где
, где  и
и  .
. , т.е. отображение вида
, т.е. отображение вида  , где любому числу (индексу)
, где любому числу (индексу)  ставится в соответствие чёткое подмножество множества Х.
ставится в соответствие чёткое подмножество множества Х. со свойствами:
со свойствами: ;
; изоморфны относительно операций
изоморфны относительно операций 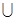 и
и  .
.


