Понятие о нечетких выводах
Нечеткие выводы – это наиболее важный метод в нечеткой логике. Многие прикладные системы, использующие промежуточные нечёткие оценки, это либо системы, основанные на правилах (нечётких продукционных правилах), либо реляционные системы, используюш\щие нечёткие отношения. Работу и тех и других систем теоретически можно объяснить с единых позиций использования композиционных правил нечетких выводов. Рассмотрим пример, как выполняются нечеткие выводы по правилам. Пусть существуют знание эксперта о том, что необходимо открыть спускной клапан, если уровень воды поднимается. Это знание можно представить в виде нечеткого продукционного правила типа «ЕСЛИ.(предпосылка, условие), ТО (заключение, действие)»: ЕСЛИ уровень воды высокий, ТО открыть клапан. (***) Понятия «высокий» и «открыть» могут интерпретироваться с помощью НМ с конкретными функциями принадлежности:
Полученные функции принадлежности можно запомнить в ЦВМ как базу знаний, т.е. можно считать что продукционые правила типа (***) накапливаются в базе знаний. Пусть также при наблюдении текущего уровня воды обнаружено, что «Уровень воды довольно высокий». Понятие «довольно высокий» может интерпретироваться с помощью НМ
Какую же «операцию» нужно проделать в такой ситуации? Т.е. возникает формула: ЕСЛИ «высокий», ТО «открыть» «довольно высокий» ------------------------------- ? Разумеется, предпосылка «высокий» и наблюдение «довольно высокий» образуются путем сопоставления. В четкой логике сопоставление не имеет смысла, поэтому никакого логического вывода сделать нельзя. Однако человек, получив путем приближенного сопоставления вывод
ЕСЛИ «высокий», ТО «открыть» «довольно высокий» -------------------------------, «Слегка открыть» должен слегка приоткрыть клапан. По сути он выполнил нечеткий вывод (точнее провел приближенные рассуждения. Для реализации приведенного нечеткого вывода (он сделан на лингвистическом уровне) с помощью функций принадлежностей существует более ста методов, которые преобразуют нечеткие выводы на лингвистическом уровне в вычисления на ЦВМ. Следует отметить, что получение конкретного значения величины управления (например, открыть клапан на 70 градусов) из НМ U «открыть» есть процесс дефазификации, т.е. преобразования НМ в чёткое представление.
|

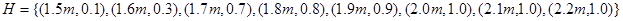 - уровни высоты воды;
- уровни высоты воды; - углы открытия клапана.
- углы открытия клапана.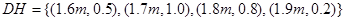 .
.


