Аналитические методы расчета
Суть методов сводится к следующему. Составляют систему уравнений по законам Кирхгофа. Поскольку характеристики нелинейных элементов, входящих в уравнения, не имеют точного аналитического описания, то их аппроксимируют (заменяют) известными аналитическими функциями, которые могут быть как линейными, так и нелинейными. Выбор аппроксимирующей функции зависит от конкретной решаемой задачи. В роли аппроксимирующих функций могут выступать степенные полиномы с заданным числом членов, а также логарифмические, экспоненциальные функции и др. Затем полученную систему уравнений решают аналитически. Ясно, что трудоемкость решения системы уравнений напрямую зависит от выбранных аппроксимирующих функций. Покажем это на следующем примере. Рассмотрим общий принцип аппроксимации степенным полиномом. Например, задана нелинейная характеристика
Рис. 2.7
Диапазон изменения аргумента В качестве аппроксимирующей функции выберем степенной полином
где Рассмотрим аппроксимацию с разными членами полинома (2.9). 1) Линейная аппроксимация
Найдем коэффициент
откуда Аппроксимирующая функция имеет вид 2) Квадратичная аппроксимация
Найдем
откуда Аппроксимирующая функция 3) Аппроксимация кубической параболой
Найдем коэффициент На рис. 2.7 функция 4) Общий случай аппроксимации степенным полиномом (2.9). Для определения трех коэффициентов из трех уравнений. На заданной характеристике Например, возьмем следующие точки, исходя из вида 1) 2) 3) Составим систему из трех уравнений (2.9) для указанных узловых точек:
или
Представим систему в стандартном виде и решим ее относительно неизвестных коэффициентов:
тогда аппроксимирующая функция примет вид
На рис. 2.7 функция (2.13) не представлена, т.к. практически совпадает с исходной зависимостью Из рассмотренных четырех вариантов аппроксимации выбирается наиболее приемлемый, исходя из требуемых критериев точности получаемых аналитических решений. Кроме того, при выборе аппроксимирующих функций необходимо учитывать симметрию исходной характеристики. Отметим, что кроме одной аппроксимирующей функции на рассматриваемом диапазоне изменения Мы рассмотрели непосредственную аппроксимацию какой-либо характеристики нелинейного элемента, кроме того, при расчете установившихся режимов в нелинейных электрических цепях применяют аппроксимацию периодических несинусоидальных функций (переменных), зависящих от времени их эквивалентными синусоидами. При этом эквивалентность может устанавливаться по их действующим значениям или по их первым гармоникам (после разложения в ряд Фурье). Такая замена позволяет применять комплексный метод расчета для большой группы нелинейных цепей переменного тока.
|

 , не имеющая точного аналитического описания, рис. 2.7.
, не имеющая точного аналитического описания, рис. 2.7.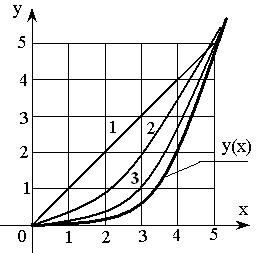
 .
.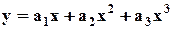 , (2.9)
, (2.9) ,
, 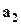 ,
,  - коэффициенты, которые требуется определить.
- коэффициенты, которые требуется определить.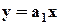 . (2.10)
. (2.10) , для этого возьмем крайнюю точку
, для этого возьмем крайнюю точку  ,
,  и подставим в уравнение (2.10):
и подставим в уравнение (2.10): ,
, .
.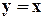 , рис. 2.7, график 1.
, рис. 2.7, график 1. . (2.11)
. (2.11) из условия, что парабола должна проходить через крайнюю точку диапазона (
из условия, что парабола должна проходить через крайнюю точку диапазона ( ):
): ,
, .
.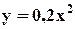 показана на рис. 2.7, график 2.
показана на рис. 2.7, график 2. . (2.12)
. (2.12)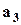 из тех же условий, что в предыдущих случаях
из тех же условий, что в предыдущих случаях 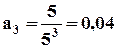 .
.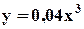 показана под номером 3.
показана под номером 3.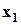 ,
,  и
и 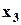 , в которых аппроксимирующая функция (2.9) и характеристика будут точно совпадать. Обычно узловые точки выбирают на заданном диапазоне и по виду характеристики
, в которых аппроксимирующая функция (2.9) и характеристика будут точно совпадать. Обычно узловые точки выбирают на заданном диапазоне и по виду характеристики 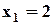 ;
; 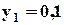 ;
;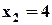 ;
;  ;
; ;
; 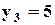 .
. ;
; ;
;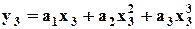 ;
;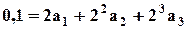 ;
;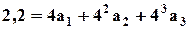 ;
;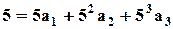 .
.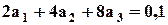 ;
; ;
;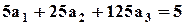 .
. ;
; 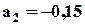 ;
; 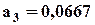 ,
, . (2.13)
. (2.13)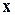 , можно выбирать несколько аппроксимирующих функций, справедливых на своем отрезке. В этом случае система уравнений решается столько раз на сколько отрезков разбит диапазон изменения
, можно выбирать несколько аппроксимирующих функций, справедливых на своем отрезке. В этом случае система уравнений решается столько раз на сколько отрезков разбит диапазон изменения 


