Электрических цепей
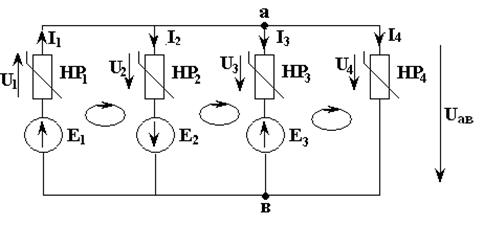
Если нелинейная разветвленная электрическая цепь имеет два узла, то за аргумент в исходной системе нелинейных алгебраических уравнений можно принять напряжение между двумя узлами. Это позволит решить графически одно нелинейное уравнение. Порядок расчета рассмотрим на примере. Пример. Дано: на рис. 3.16 представлена нелинейная электрическая цепь в виде схемы замещения; на рис. 3.17 - в первом квадранте ВАХ нелинейных резистивных элементов; Е1, Е2 и Е3. Найти: все токи I1 , I2, I3, I4 и падения напряжения на нелинейных элементах U1, U2, U3, U4.
Рис. 3.16
Решение. 1) Составим систему уравнений по законам Кирхгофа:
2) За функции примем токи в ветвях, а за аргумент напряжение между двумя узлами Uaв. С учетом сказанного, исходную систему уравнений (3.12) можно представить в следующем виде. Для этого перепишем первое уравнение системы в виде функций от напряжения Uaв:
Рис. 3.17
Ампер-вольтные характеристики уравнения (3.13) будем строить по формулам, полученным с помощью второго закона Кирхгофа. Для этого составим уравнения для четырех контуров (см. рис. 3.16 и 3.18), образованных вектором Uaв и первой ветвью,
вектором Uaв и второй ветвью,
вектором Uaв и третьей ветвью,
вектором Uaв и четвертой ветвью,
Из уравнений (3.14) – (3.17) получим зависимости для требуемых ВАХ:
Рис. 3.18 Используя графики рис. 3.17 и заданные ЭДС, построим ВАХ по (3.18), которые представлены на рис. 3.19 как
Рис. 3.19
3) Решим уравнение (3.13) графически, см. рис. 2.1. На рис. 3.19 построим график правой части уравнения (3.13): Uав I1(Uав) I1;
По полученным значениям токов и по ВАХ рис. 3.17 находим падения напряжения на нелинейных резисторах:
где к = 1,2,3,4. Отметим, что рабочая точка а может лежать в любом квадрате. Так как ВАХ нелинейного резистивного элемента симметрична относительно начала координат (рис. 3.17), то при нахождении рабочей точки а можно достроить недостающие части ВАХ с учетом указанной симметрии. Значения токов и напряжения между двумя узлами снимаются с соответствующих осей со своими знаками.
|

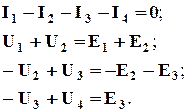 (3.12)
(3.12) . (3.13)
. (3.13)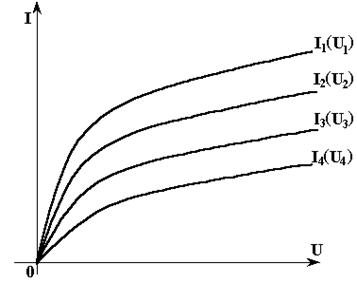
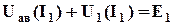 ; (3.14)
; (3.14)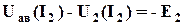 ; (3.15)
; (3.15)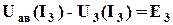 ; (3.16)
; (3.16)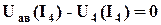 . (3.17)
. (3.17)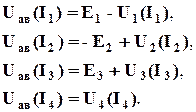 (3.18)
(3.18)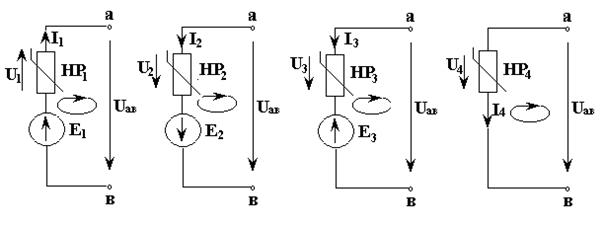
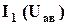 ,
,  ,
,  и
и 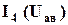 соответственно.
соответственно.
 . Точка а пересечения этого суммарного графика с графиком левой части уравнения (3.13) и будет рабочей точкой, из которой опускаем перпендикуляр на ось абсцисс и находим значение напряжения
. Точка а пересечения этого суммарного графика с графиком левой части уравнения (3.13) и будет рабочей точкой, из которой опускаем перпендикуляр на ось абсцисс и находим значение напряжения 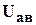 , затем по следующему алгоритму определим токи:
, затем по следующему алгоритму определим токи: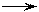



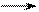
 I3(Uав) I3;
I3(Uав) I3;