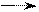Смешанное соединение элементов
В предыдущих разделах графически решалось одно уравнение. В этом разделе будем решать графически систему нелинейных уравнений. Пример 1. Заданы нелинейная электрическая схема, ВАХ нелинейных элементов и входное напряжение U=U0. Требуется найти все токи в ветвях и падение напряжения на элементах, рис. 3.13.
а) б)
Рис. 3.13
Решение. 1) Составим систему уравнений по законам Кирхгофа: I1=I2+I3, U1+Uab=U, U2=U3=Uab. В зависимости от вида соединения элементов (см. разделы 3.1.1. и 3.1.2.), выберем аргументы и перепишем систему (3.10) в следующем виде:
Первое уравнение системы (3.11) соответствует замене параллельного участка схемы рис. 3.13а, а второе определяет эквивалентную ВАХ всей схемы при последовательном соединении элементов. Указанные эквивалентные преобразования исходной схемы рис. 3.13а приведены на рис. 3.14. 2) Найдем ампер-вольтную характеристику I1(Uab) эквивалентного нелинейного сопротивления HP23, рис. 3.14а, по первому уравнению системы (3.11). Здесь и далее построения будем делать на рис. 3.15. 3) Схему рис. 3.14а преобразуем в схему рис. 3.14б, для этого найдем результирующую вольт-амперную характеристику U(I1) по второму уравнению системы (3.11). У полученной в п. 2 зависимости I1(Uab) аргумент и функцию поменяем местами, тогда, давая значения току I1, сложим напряжения U1(I1) и Uab(I1). Полученная таким образом ВАХ U(I1) соответствует схеме рис. 3.14б.
а) б)
Рис. 3.14
Рис. 3.15
3) На рис. 3.15 реализован следующий алгоритм нахождения требуемых значений токов и падений напряжений:
Пример 2. Используя данные и построения предыдущего примера, необходимо написать алгоритм определения остальных токов и напряжений при заданных: a) I1=I10 и б) I3=I30. Решение. a) Напишем алгоритм при условии п.а. Для этого используем схемы рис. 3.14а и 3.13а, а также соответствующие построения рис. 3.15:
б) Для условия п.б алгоритм решения примет следующий вид:
Из приведенного алгоритма видно, что при таком условии задачи не требуется преобразовывать исходную схему в схемы рис. 3.14, а достаточно использовать заданные ВАХ элементов, рис. 3.13б.
|

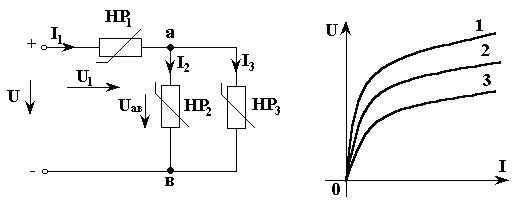
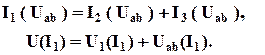 (3.11)
(3.11)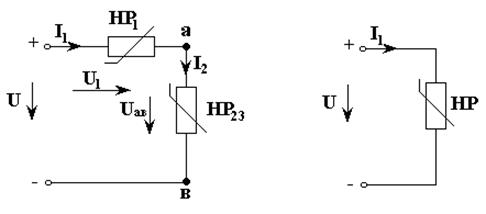




 I10 Uав(I1) Uав,0 I2(Uав) I20;
I10 Uав(I1) Uав,0 I2(Uав) I20;
 U1(I1) U10; I3(Uав) I30.
U1(I1) U10; I3(Uав) I30.