Графические методы расчета
Применяются для расчета простых нелинейных электрических цепей, содержащих, как правило, однотипные элементы. Основаны на графическом решении нелинейных алгебраических уравнений. Решение получают на плоскости (х, y), в которой аргумент х и функция у, по мере решения системы уравнений, могут меняться местами.
Например, аргумент х и функции
здесь
Рис. 2.1
При решении уравнения (2.1) можно применить два метода: метод преобразования и метод пересечения характеристик. Рассмотрим каждый метод. Метод преобразования характеристик основан на том, что, согласно (2.1), строится результирующая функция
того же аргумента, рис.2.2, по которой при заданном значении правой части уравнения (2.1)
Рис. 2.2
На рис.2.2, после построения зависимости
Метод пересечения характеристик основан на построении двух графиков – левой и правой частей уравнения (2.2). Точка пересечения этих графиков будет решением уравнения. Допустим, уравнение (2.1) можно представить в виде
На рис.2.3 показано решение уравнения (2.3) как точка
Рис. 2.3
Рассмотрим графический метод расчета, когда аргумент и функция (функции) зависят от времени t. Решим графически уравнение
или (2.5)
где
Для решения уравнения (2.5) воспользуемся методом преобразования: - найдем графически результирующую характеристику, согласно (2.5), как
Рис. 2.4
- по заданной функции
между временем
где
Рис. 2.5
При этом масштабы по осям - по полученному графику
Рис. 2.6
Если правая часть уравнения (2.5)
|

 и
и 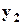 не зависят от времени (постоянный ток) и решаемое нелинейное алгебраическое уравнение имеет вид
не зависят от времени (постоянный ток) и решаемое нелинейное алгебраическое уравнение имеет вид , (2.1)
, (2.1)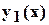 и
и  - нелинейные зависимости, заданные в виде графиков, рис.2.1;
- нелинейные зависимости, заданные в виде графиков, рис.2.1; 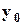 - константа.
- константа.
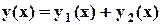
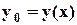 находим значение аргумента
находим значение аргумента 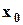 и по графикам
и по графикам 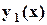 и
и 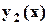 значения функции
значения функции  и
и  .
.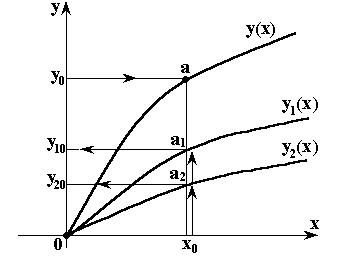
 , стрелками показано решение уравнения (2.1), т.е. реализован следующий алгоритм:
, стрелками показано решение уравнения (2.1), т.е. реализован следующий алгоритм:

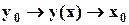 (2.2)
(2.2)
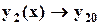 .
. . (2.3)
. (2.3)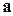 пересечения двух графиков
пересечения двух графиков 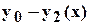 . Стрелками показан алгоритм нахождения требуемых величин
. Стрелками показан алгоритм нахождения требуемых величин  :
: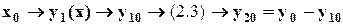 . (2.4)
. (2.4)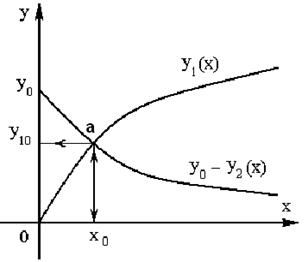
 ,
, ,
, - нелинейные зависимости, симметричные относительно начала координат, представленные на рис. 2.4;
- нелинейные зависимости, симметричные относительно начала координат, представленные на рис. 2.4; - заданная периодическая функция времени
- заданная периодическая функция времени  , здесь Т – период.
, здесь Т – период.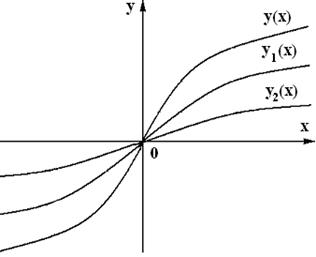
 (2.6)
(2.6) и аргументом
и аргументом 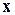 , находим графически зависимость
, находим графически зависимость 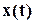 по следующему алгоритму:
по следующему алгоритму: , (2.7)
, (2.7) - дискретное значение времени на интервале
- дискретное значение времени на интервале 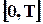 ,
,  , рис. 2.5.
, рис. 2.5.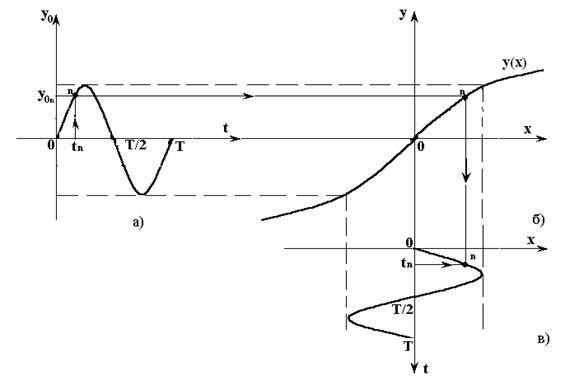
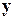 и
и 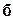 ,
, 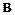 выбирают обычно одинаковыми;
выбирают обычно одинаковыми; и
и 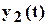 , при этом алгоритм построения имеет следующий вид, рис.2.6:
, при этом алгоритм построения имеет следующий вид, рис.2.6:
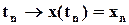 (2.8)
(2.8)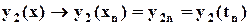

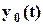 будет состоять, например, из постоянной и периодической составляющих, то это отразится на рис. 2.5а как поднятие показанной периодической составляющей (или ее опускание) на величину постоянной составляющей, а алгоритм построения остается прежним. Ясно, что в этом случае решения
будет состоять, например, из постоянной и периодической составляющих, то это отразится на рис. 2.5а как поднятие показанной периодической составляющей (или ее опускание) на величину постоянной составляющей, а алгоритм построения остается прежним. Ясно, что в этом случае решения  и
и 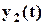 будут отличными от полученных на рис. 2.5 и рис. 2.6.
будут отличными от полученных на рис. 2.5 и рис. 2.6.


