Расчет разветвленной магнитной цепи
Рассмотрим два примера расчета разветвленной магнитной цепи, имеющей два узла. Пример 1. На рис.4.4а задана магнитная цепь. Конструктивные размеры l1, l2, l3 и S1, S2, S3, а также основная кривая намагничивания В(Н), рис.4.4б, значение потока Ф3 = Ф30 . Требуется найти магнитодвижущую силу F, потоки Ф1, Ф2 и падение магнитного напряжения Uм,ab.
Таблица 4.1
А) б) Рис. 4.4
Решение. 1. Нарисуем схему замещения, рис. 4.5.
Рис. 4.5 2. По законам Кирхгофа для магнитных цепей запишем систему уравнений в удобном для решения виде:
3. Запишем алгоритм решения системы (4.8) в виде:
Из приведенного алгоритма видно, что дополнительные графики строить не требуется. В алгоритме используется только график основной кривой намагничивания В(Н), рис. 4.4б. Все требуемые значения Ф1, Ф2, Uм,aв и F будут найдены при реализации приведенного алгоритма. Пример 2. Задана магнитная цепь, рис. 4.6, основная кривая намагничивания В(Н) материала магнитопровода, рис. 4.7, конструктивные данные магнитопровода и катушек, табл. 4.2. Требуется найти магнитные потоки в сердечнике Ф1, Ф2 и Ф3.
Рис. 4.6
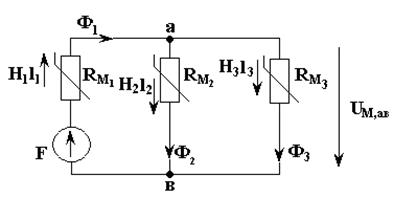
Решение. 1. По исходной схеме рис. 4.6 нарисуем схему замещения, рис. 4.8. Выберем направления магнитных потоков, затем укажем падения напряжения на участках магнитопровода.
Рис. 4.7
Рис. 4.8
2. Запишем систему уравнений по законам Кирхгофа:
3. Для графического решения системы нелинейных уравнений (4.9) воспользуемся методом двух узлов, см. р. 3.1.4. За функции выберем магнитные потоки Ф1, Ф2 и Ф3, за аргумент примем напряжение между двумя узлами Udk. Тогда первое уравнение системы (4.9) можно записать в следующем виде: Ф1(Udk)+Ф3(Udk)=Ф2(Udk),(4.10) где соответствующую зависимость потока от падения магнитного напряжения найдем на основе второго закона Кирхгофа при рассмотрении трех контуров, рис. 4.9.
Рис. 4.9 Для контуров рис. 4.9 имеем:
Здесь аргумент и функции поменялись местами: F1=w1I1, F3=w3I3 и F4=w4I4. Для построения зависимости магнитного потока на участках магнитопровода по (4.11) воспользуемся электронными таблицами Excel, табл. 4.3. В табл. 4.3 первые два столбца отображают основную кривую намагничивания В(Н), сокращены обозначения для падения магнитного напряжения: Udk1= Udk(Ф1), Udk2= Udk(Ф2) и Udk3= Udk(Ф3). По данным табл. 4.3 построены соответствующие графики рис. 4.10 - 4.12.
Рис. 4.10
Рис. 4.11
Рис. 4.12
Рис. 4.13
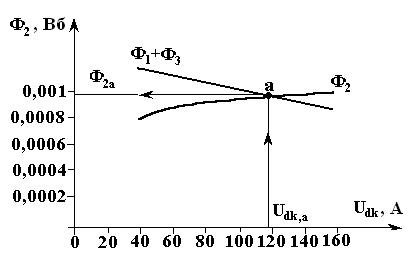
На рис. 4.13 показано графическое решение уравнения (4.10). В точке а пересечения графиков Ф2 и Ф1 + Ф3 выполняется уравнение (4.10). Таблица 4.2
Таблица 4.3
Согласно построения рис. 4.13, определяем значение магнитного напряжения Udk,a=118 А и магнитный поток Ф2а = 0,00095 Вб. Для определения потоков Ф1 и Ф3 реализуем следующий алгоритм, используя рис. 4.10 и 4.12:
Проверим правильность найденных значений магнитных потоков по уравнению (4.10). Допустим, что полученная точность решения нас удовлетворяет, в противном случае, надо добиваться требуемой точности.
|



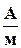

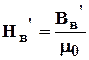


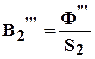


 (4.8)
(4.8)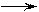
 B(H) H3 Uм,aв = H3l3
B(H) H3 Uм,aв = H3l3


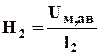 B(H) B2 Ф2=B2S2 Ф1=Ф2+Ф3
B(H) B2 Ф2=B2S2 Ф1=Ф2+Ф3 B(H) H1 F=H1l1+ Uм,aв.
B(H) H1 F=H1l1+ Uм,aв.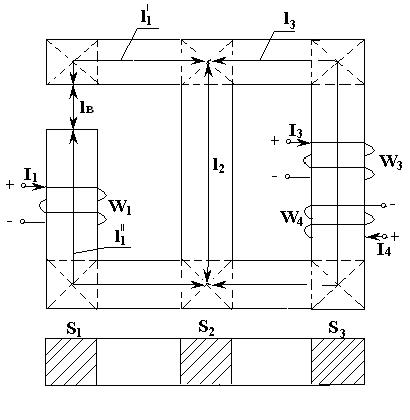


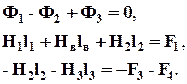 (4.9)
(4.9)
 (4.11)
(4.11)



 Ф3(Udk) Ф3а=0,00059 Вб.
Ф3(Udk) Ф3а=0,00059 Вб.


