Расчет постоянного магнита с воздушным зазором
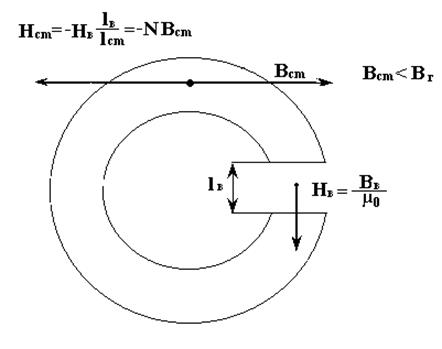
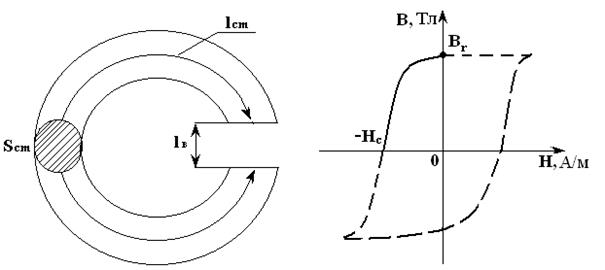
На рис. 4.14 показан кольцевой постоянный магнит с воздушным зазором. Сердечник магнита выполнен из магнитотвердой стали, длина воздушного зазора lв значительно меньше длины сердечника lc. Сталь намагничена до насыщения. Заданы площадь сечения Scm и длины участков lcm и lв магнитопровода, кривая размагничивания В(Н), рис. 4.15. Требуется найти магнитный поток в воздушном зазоре.
Рис. 4.14 Рис. 4.15
При отсутствии воздушного зазора по второму закону Кирхгофа для магнитной цепи имеем Нcmlcm=0. Отсюда следует, что напряженность магнитного поля в стальном сердечнике будет равна нулю Нcm=0, а индукция в сердечнике будет равна остаточной Вcm=Вr, согласно графика рис. 4.15. Запишем уравнение по второму закону Кирхгофа для магнитной цепи с воздушным зазором, рис. 4.14, Нcmlcm +Hвlв = 0, (4.12) из которого найдем напряженность магнитного поля в сердечнике
В формуле (4.13) сделаем следующие подстановки:
где µ0= 4π10-7 Гн/м; Вв = Вcm,т.к. в магнитопроводе один и тот же магнитный поток Ф и сечение воздушного зазора принимаем равным сечению сердечника Sв=Sсm ( Тогда формула (4.13) примет вид
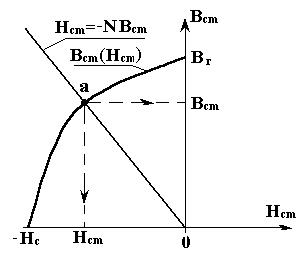
где коэффициент размагничивания На рис. 4.15 показаны направления векторов напряженности и индукции магнитного поля в магнитопроводе. При этом выполняются соотношения: из формулы (4.14) следует, что Нcm<0, (4.16) тогда Вcm=Bв<Вr=µ0J, (4.17) т. к. Вcm=µ0J+µ0Hcm= Вr+µ0·Hcm,где J -вектор намагниченности стали. Отсюда следует, что рабочая точка с координатами Нсm<0 и Bcm<Br будет лежать на кривой размагничивания В(Н) (во втором квадранте), рис.4.15. Решим графически систему уравнений, состоящую из линейного уравнения (4.14) и кривой размагничивания В(Н), представленной на рис. 4.15: Нcm= - N Вcm, (4.18) Вcm(Нcm). (4.19) Находим коэффициент размагничивания по формуле (4.15), используя конструктивные размеры магнитопровода:
Рис. 4.16
Найденное значение N подставим в уравнение (4.18). В одной системе координат нарисуем графики зависимостей (4.18) и (4.19). Точка пересечения графиков дает рабочую точку а, рис. 4.17. Находим ее координаты Нст и Вст, затем, согласно постановки задачи, находим магнитный поток в воздушном зазоре Ф=ВвSв= ВcmScm.
Рис. 4.17
|

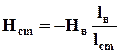 . (4.13)
. (4.13)
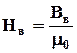 ,
,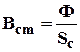 ,
, 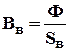 ).
).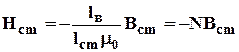 ,(4.14)
,(4.14)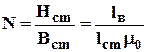 . (4.15)
. (4.15)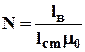 .
.