Графический метод расчета по мгновенным значениям
Применяется для расчета простых нелинейных электрических цепей, содержащих однородные элементы, например, только нелинейные резистивные элементы (НР), или нелинейные индуктивные элементы (НИ),или нелинейные емкостные элементы (НЕ), см. р. 2.1.
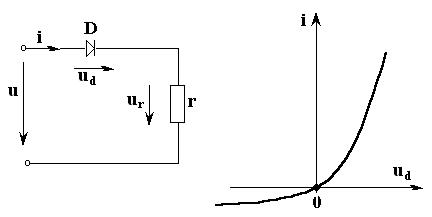
Пример 1. На рис. 5.1 показана электрическая цепь в виде схемы замещения, ВАХ диода представлена на рис. 5.2,
Рис. 5.1 Рис. 5.2
заданы значения сопротивления r и закон изменения входного напряжения u=Umsin(ωt). Требуется построить графики изменения тока i, напряжений на элементах ud и ur от времени. Решение сводится к графической реализации следующего алгоритма: 1. Найдем результирующую ВАХ всей цепи, составив уравнение по второму закону Кирхгофа, рис. 5.1,
или u(i)=ud(i)+rI, (5.2)
где ud(i) - ВАХ диода, рис.5.2.
1. Построим результирующую ВАХ (или i(U) – ампер-вольтную характеристику) по (5.2), рис. 5.3.
Рис. 5.3
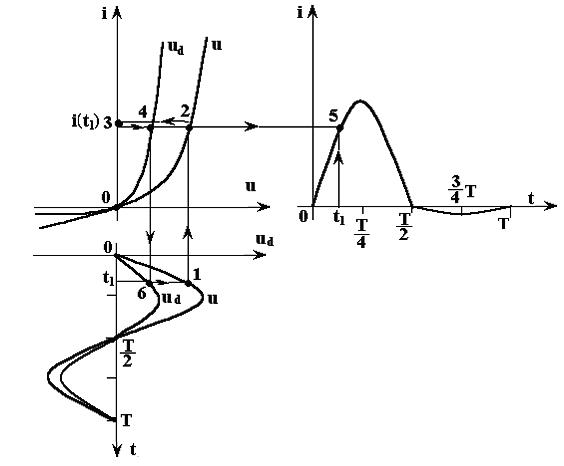
3. Затем графически реализуем алгоритм, рис. 5.4:
здесь tn На рис.5.4 масштабы по одноименным осям выбраны одинаковыми. Стрелками и цифрами от 1 до 6 показан один цикл построения. График изменения напряжения на резисторе ur аналогичен закону изменения тока, поэтому график ur не приводится.
Рис. 5.4
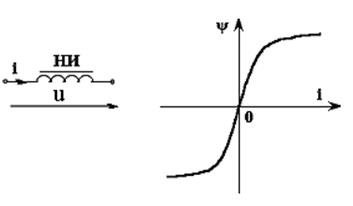
Пример 2 На рис. 5.5 показана схема с нелинейной индуктивностью, по которой протекает синусоидальный ток i=Imsin(ωt),на рис. 5.6 показана её вебер-амперная характеристика ψ(i). Требуется построить кривую изменения падения напряжения на нелинейной индуктивности u(t).
Рис. 5.5 Рис. 5.6
Запишем алгоритм решения в виде цепочки:
где tn Реализуем алгоритм на графиках рис. 5.7.
Рис. 5.7
Падение напряжения на нелинейной индуктивности u(t) получено путем дифференцирования кривой потокосцепления ψ(t).
|

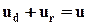 ,(5.1)
,(5.1)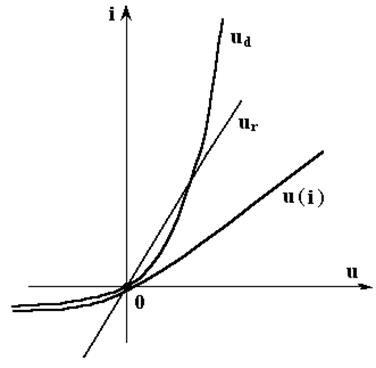
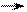
 tn u[tn] i(u) i[tn] ur[tn]=r·i[tn] (5.3)
tn u[tn] i(u) i[tn] ur[tn]=r·i[tn] (5.3) ud(i) ud[tn];
ud(i) ud[tn]; [0,T] дискретные значения времени на периоде
[0,T] дискретные значения времени на периоде 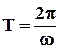 .
.


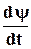 , (5.4)
, (5.4) .
.



