Метод расчета по действующим значениям несинусоидальных напряжений и токов или по их первым гармоникам
Суть метода расчета по действующим значениям напряжения и тока сводится к тому, что несинусоидальные напряжения и токи заменяются эквивалентными синусоидальными напряжениями и токами. Эквивалентность устанавливается по их действующим значениями. Например, для несинусоидального тока можно записать действующее значение Затем
Здесь
Зависимость между напряжением и током устанавливается по действующим значениям. Фазовый сдвиг между напряжением и током на нелинейных сопротивлениях (элементах) будет точно таким же, как для аналогичных линейных сопротивлениях (элементах). Величины сопротивлений и параметры нелинейных элементов для рабочих точек могут быть усреднены, например, для нелинейной катушки индуктивности для рабочей точки а на ВАХ имеем, рис. 5.14,
где
Рис. 5.14
В комплексной форме записи, с учетом принятых допущений, можно записать при для нелинейной индуктивного элемента
где для нелинейного емкостного элемента
где для нелинейного резистивного элемента
где Здесь Если при расчете используются усредненные параметры для конкретной рабочей точки ВАХ, то вместо нелинейных элементов получим соответствующие линейные элементы. При смене режима работы цепи необходимо для новой рабочей точки найти новые параметры линейных элементов. Таким образом, для расчета и анализа нелинейных электрических цепей переменного тока можно применять комплексный метод расчета. Метод расчета по первым гармоникам несинусоидальных напряжений и токов аналогичен предыдущему методу. Разница состоит только в том, что в этом случае эквивалентами несинусоидальных напряжения и тока выступает их первая гармоника, которая находится после их разложения в ряд Фурье. При расчете используют ВАХ, построенную по первым гармоникам напряжения и тока. Рассматриваемые методы широко используются для расчета электрических цепей, содержащих катушку с ферромагнитным сердечником, электрических машин, для анализа феррорезонансных явлений. Рассмотрим порядок расчета на некоторых характерных примерах. Пример 1. Задана нелинейная электрическая цепь, рис. 5.15, вольтамперная характеристика нелинейной катушки индуктивности, построенная по действующим значениям напряжения и тока, рис. 5.16, величина сопротивления линейного резистора
Рис. 5.15
Решение. 1. Составим уравнение по второму закону Кирхгофа для мгновенных значений падения напряжения и тока
или
Будем считать, что вместо несинусоидального тока
или (5.22)
2. Для решения комплексного нелинейного уравнения (5.22) воспользуемся графическим методом расчета в сочетании с аналитическим. Построим зависимость тока от входного напряжения, по которой найдем требуемые законы изменения тока и падения напряжения на нелинейной катушке индуктивности. Для построения указанных зависимостей реализуем следующий алгоритм. Направим вектор тока по вещественной оси
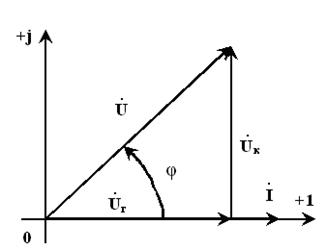
Первое значение тока выберем вначале ВАХ, т.е. близкое к нулю. На рис. 5.16 представлена векторная диаграмма напряжений, совмещенных с векторной диаграммой тока.
Рис. 5.16
Ясно, что алгоритм (5.23) может быть реализован графически в виде векторных диаграмм для выбранных значений тока. При реализации алгоритма (5.23) значения току даем до тех пор, пока модуль вычисленного напряжения
Рис. 5.17
3. По заданному входному напряжению
Определим начальную фазу для тока, т.к. в начальной посылке мы сделали ее нулевой, а реальная таковой не будет. Например, определим ее на построенной ранее векторной диаграмме рис. 5.16. Начальная фаза входного напряжения по условию задачи нулевая, тогда, согласно векторной диаграмме рис. 5.16, направим вещественную ось +1 по вектору напряжения, рис. 5.18.
Рис. 5.18
По векторной диаграмме рис. 5.18 определим все требуемые векторы. Тогда комплекс действующего значения тока будет Запишем закон изменения тока
Аналогичные выкладки приведут к закону изменения напряжения на катушке
где Отметим, что полученные законы (5.25) и (5.26) соответствуют эквивалентным синусоидам.
Пример 2. На рис. 5.19 представлена схема с нелинейным емкостным элементом. Вольт-амперная характеристика емкостного элемента получена по первым гармоникам напряжения, тока и приведена на рис. 5.20. Сопротивление резистора Входное напряжение изменяется по синусоидальному закону, действующее значение которого Требуется найти комплекс действующих значений токов и падений напряжений.
Рис. 5.19
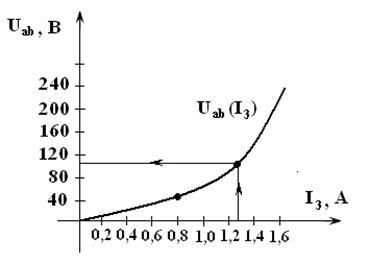
Рис. 5.20
Решение. Составим систему уравнений по законам Кирхгофа в комплексной форме записи. При этом систему уравнений запишем в удобном для решения виде:
Так как задана ВАХ Тогда алгоритм решения сводится к следующему:
Реализуем алгоритм (5.28) для следующих значений тока, рис. 5.20: 1.
2.
3.
По полученным в п.2 данным построим графическую зависимость
Рис. 5.21
Для найденного значения тока
Небольшое расхождение ( По уравнениям (5.27) построим векторные диаграммы напряжений и токов для полученного решения, рис. 5.22. Поясним определение начальных фаз и полученных падений напряжения и токов в зависимости от начальной фазы заданного входного напряжения
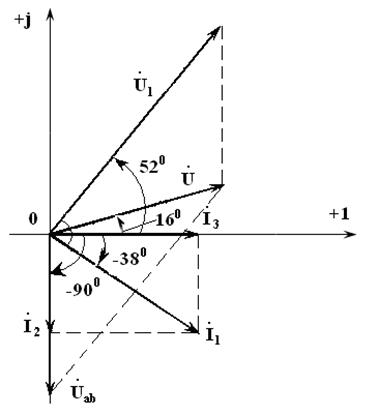
Рис. 5.22:
Так как третий ток направлен по вещественной оси
Рис. 5.23
После пересчета начальных фаз токов и падений напряжений, согласно диаграмм рис. 5.23, ответ запишется:
Мы рассмотрели пример расчета, когда электрическая цепь содержала нелинейный емкостной элемент. Методика решения остается прежней, если в электрической цепи нелинейным, например, будет индуктивность или резистор.
|

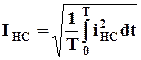 .
.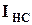 принимаем равными действующему значению синусоидального тока, поэтому эквивалентный синусоидальный ток будет изменяться по закону
принимаем равными действующему значению синусоидального тока, поэтому эквивалентный синусоидальный ток будет изменяться по закону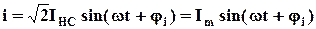 . (5.20)
. (5.20) - амплитудное значение синусоидального тока;
- амплитудное значение синусоидального тока;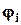 - начальная фаза несинусоидального тока;
- начальная фаза несинусоидального тока;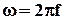 - угловая частота, совпадает с частотой несинусоидального тока.
- угловая частота, совпадает с частотой несинусоидального тока.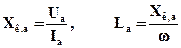 ,
,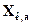 и
и 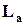 - величины сопротивления и индуктивности катушки для рабочей точки а.
- величины сопротивления и индуктивности катушки для рабочей точки а.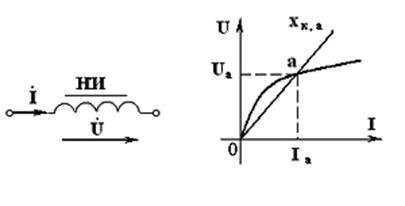
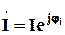 :
: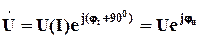 ,
,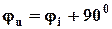 ;
;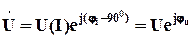 ,
,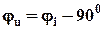 ;
;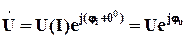 ,
,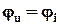 .
.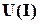 - вольт-амперная характеристика по действующим значениям несинусоидальных тока и напряжения.
- вольт-амперная характеристика по действующим значениям несинусоидальных тока и напряжения.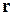 и закон изменения входного напряжения
и закон изменения входного напряжения 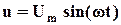 . Требуется найти закон изменения тока и падения напряжения на нелинейной катушке индуктивности.
. Требуется найти закон изменения тока и падения напряжения на нелинейной катушке индуктивности.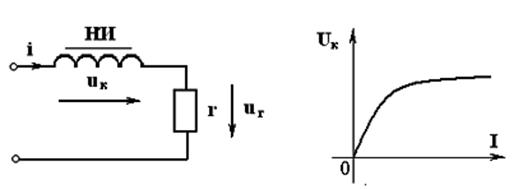
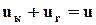 ,
,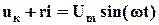 . (5.21)
. (5.21)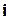 будет течь эквивалентный по действующему значению синусоидальный ток. Такое допущение позволяет переписать уравнение (5.21) в комплексной форме записи:
будет течь эквивалентный по действующему значению синусоидальный ток. Такое допущение позволяет переписать уравнение (5.21) в комплексной форме записи: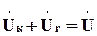 ,
,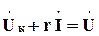 .
.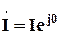 , модулю тока будем давать значения в диапазоне его изменения, согласно ВАХ нелинейной катушки индуктивности, рис. 5.15, и определять остальные векторы по алгоритму:
, модулю тока будем давать значения в диапазоне его изменения, согласно ВАХ нелинейной катушки индуктивности, рис. 5.15, и определять остальные векторы по алгоритму:


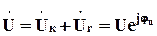 . (5.23)
. (5.23)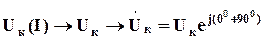
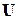 не превысит действующего значения заданного входного напряжения
не превысит действующего значения заданного входного напряжения 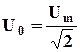 . Затем строим результирующую характеристику – зависимость действующего значения тока
. Затем строим результирующую характеристику – зависимость действующего значения тока 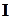 от действующего значения входного напряжения
от действующего значения входного напряжения 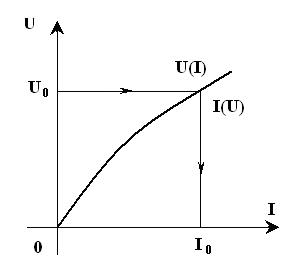
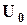 находим ток
находим ток 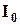 , рис. 5.17. Затем для найденного значения тока
, рис. 5.17. Затем для найденного значения тока 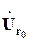 ,
, 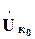 и
и 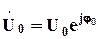 . (5.24)
. (5.24)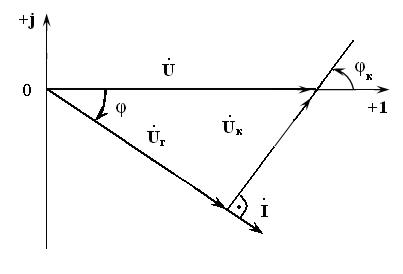
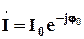 , где
, где 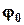 - соответствует значению (5.24).
- соответствует значению (5.24).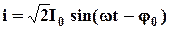 . (5.25)
. (5.25)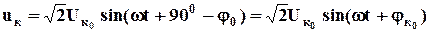 , (5.26)
, (5.26)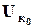 и
и 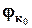 - соответственно модуль и фаза напряжения на катушке, полученные для тока
- соответственно модуль и фаза напряжения на катушке, полученные для тока 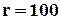 Ом, сопротивление индуктивного элемента для первой гармоники
Ом, сопротивление индуктивного элемента для первой гармоники  Ом.
Ом. В.
В.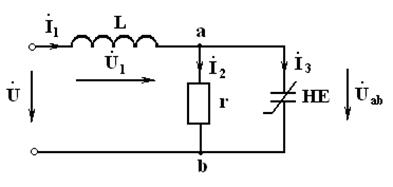
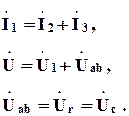 (5.27)
(5.27)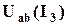 , то решение задачи начнем с построения зависимости входного напряжения
, то решение задачи начнем с построения зависимости входного напряжения 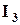 . При построении указанной ВАХ используем систему комплексных нелинейных уравнений (5.27). Для определенности направим вектор
. При построении указанной ВАХ используем систему комплексных нелинейных уравнений (5.27). Для определенности направим вектор  по вещественной оси, т.е.
по вещественной оси, т.е. 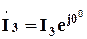 .
. (5.28)
(5.28)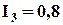 А;
А;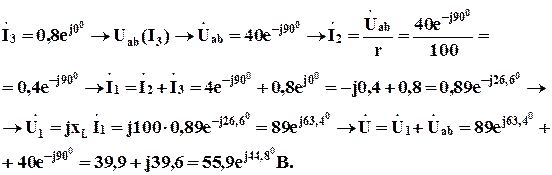
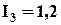 А;
А;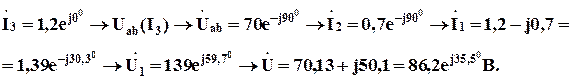
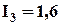 А;
А;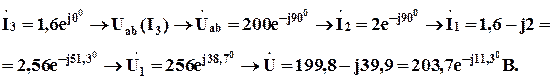
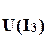 , см. рис. 5.21, по которой определим модуль третьего тока:
, см. рис. 5.21, по которой определим модуль третьего тока: В
В 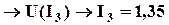 А.
А.
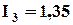 А реализуем алгоритм (5.28)
А реализуем алгоритм (5.28)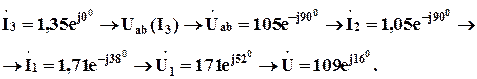
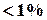 ) между заданным входным напряжением (110 В) и полученным (109 В) будем считать допустимым.
) между заданным входным напряжением (110 В) и полученным (109 В) будем считать допустимым.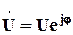 .
.
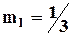 А/см;
А/см; 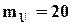 В/см
В/см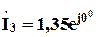 , то у входного напряжения начальная фаза в результате реализации алгоритма (5.28) получается отличной от заданной,
, то у входного напряжения начальная фаза в результате реализации алгоритма (5.28) получается отличной от заданной, 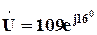 , поэтому необходимо повернуть относительно начала координат полученные векторные диаграммы напряжений и токов на 160 (таким образом, чтобы вектор входного напряжения
, поэтому необходимо повернуть относительно начала координат полученные векторные диаграммы напряжений и токов на 160 (таким образом, чтобы вектор входного напряжения 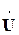 совпадал по направлению с вещественной осью), что будет соответствовать нулевой начальной фазе входного напряжения, рис. 5.23.
совпадал по направлению с вещественной осью), что будет соответствовать нулевой начальной фазе входного напряжения, рис. 5.23.
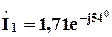 ;
; 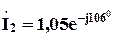 ;
; 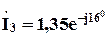 ;
; ;
;  .
.


