Нечеткие и лингвистические переменные
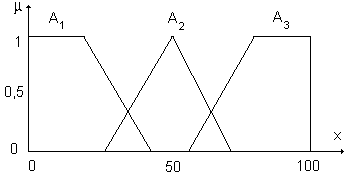
Понятия нечеткой и лингвистической переменных используются при задании входных и выходных переменных в системах управления с использованием аппарата нечеткой логики. Нечеткая переменная задается кортежем <α, X, A>;, где α; — имя переменной; X — область определения этой переменной (универсум); А = <x, µA(x)> — нечеткое множество на X, описывающее возможные значения нечеткой переменной. Лингвистическая переменная представляет собой переменную, значение которой определяется набором вербальных (словесных) характеристик некоторого свойства. Например, лингвистическая переменная "давление" определяется через набор {очень низкое, низкое, среднее, высокое, очень высокое}. Значения лингвистической переменной (ЛП) определяются через нечеткие множества, которые, в свою очередь, определяются на некотором базовом наборе значений или базовой числовой шкале, имеющей размерность. Каждое значение ЛП определяется как нечеткое множество, например, нечеткое множество "высокое давление". Лингвистической переменной называется набор <β, Т, X, G, М>;, где: β – наименование лингвистической переменной; Т – базовое множество (терм-множество) значений (термов) лингвистической переменной, представляющих собой наименования отдельных нечетких переменных α;; G – синтаксическая процедура, позволяющая оперировать элементами терм-множества Т, в частности, генерировать новые термы (значения) G(T). При этом множество Т È G(T) называется расширенным терм-множеством лингвистической переменной; М – семантическая процедура, позволяющая преобразовать каждое новое значение лингвистической переменной, образуемое процедурой G, в нечеткую переменную, т.е. сформировать соответствующее нечеткое множество. Пример. Пусть эксперт определяет температуру жидкости с помощью понятий «Малая температура», «Средняя температура» и «Большая температура», при этом минимальная температура равна 0 градусов, а максимальная – 100 градусов. Формализация такого описания может быть проведена с помощью лингвистической переменной <β, Т, X, G, М>;, где β – температура жидкости; Т – {«Малая температура», «Средняя температура», «Большая температура»}; X – [0, 100]; G – процедура образования новых термов с помощью связок «и», «или» и модификаторов типа «очень», «не», «слегка» и т.п. Например: «Малая или средняя температура», «Очень малая температура» и т.д.; М – процедура задания на X = [0, 100] нечетких подмножеств А1 = «Малая температура», А2 = «Средняя температура», А3 = «Большая температура», а также нечетких множеств для термов из G(T) в соответствии с правилами трансляции нечетких связок и модификаторов «и», «или», «не», «очень», «слегка» и других операций над нечеткими множествами вида: А Ç В, A È B, Замечание. Наряду с рассмотренными выше базовыми значениями лингвистической переменной «температура» (Т = {«Низкая температура», «Средняя температура», «Высокая температура»}) возможны значения, зависящие от области определения X. Так, значения лингвистической переменной «Температура жидкости» можно определить как «около 0 градусов», «около 50 градусов», «около 100 градусов», т.е. в виде нечетких чисел. Терм-множество и расширенное терм-множество для нашего примера можно характеризовать функциями принадлежности, приведенными на рис. 1.3 и 1.4. На рис. 1.3 приведены функции принадлежности нечетких множеств A1= «Низкая температура», A2 = «Средняя температура» и A3 = «Высокая температура», которые составляют терм-множество.
Рис. 1.3. Функции принадлежности терм-множества
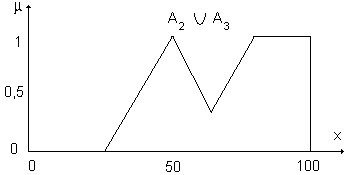
На рис. 1.4 приведена функция принадлежности нечеткого множества A2 È A3 = «Средняя или высокая температура», которое может в составе расширенного терм-множества.
Рис. 1.4. Функция принадлежности нечеткого множества A2 È A3 Отметим, что функция принадлежности отличается от вероятности, которая имеет объективный характер и подчиняется другим математическим зависимостям. Функция принадлежности обычно зависит от мнения экспертов, участвующих в определении нечеткого множества. Например, для двух экспертов определение нечеткого множества "высокая" для лингвистической переменной "цена автомобиля" может заметно отличаться: "высокая_цена_автомобиля_1"={50000/1+25000/0,8+10000/0,6+5000/0,4}. "высокая_цена_автомобиля_2"={25000/1+10000/0,8+5000/0,7+3000/0,4}. Пример. Лингвистическая переменная "возраст". Пусть требуется интерпретация значений лингвистической переменной "возраст", таких как "младенческий" и "детский". Базовый набор значений логической переменной "возраст" может быть определен следующим образом:
В={"младенческий", "детский", "юный", "молодой", "зрелый", "преклонный"}.
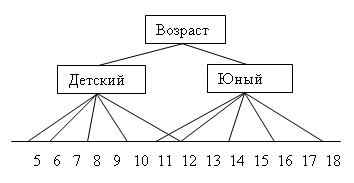
Для логической переменной "возраст" базовую шкалу представляет числовая шкала прожитых лет от 0 до 120, а функция принадлежности определяет степень уверенности в том, что данное количество лет можно отнести к данной категории возраста. На рис. 1.5 показана схема формирования нечетких множеств логической переменной "возраст".
Рис. 1.5. Схема формирования нечетких множеств Как видим, одни и те же значения базовой шкалы могут участвовать в определении различных нечетких множеств.
|

 , CON A = A2, DIL A = A0,5 и т.п.
, CON A = A2, DIL A = A0,5 и т.п.