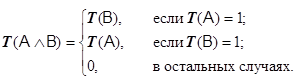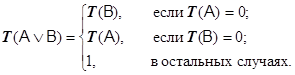Логические операции с нечеткими высказываниями
Для рассмотрения логических операций с нечеткими высказываниями обозначим: U — некоторое множество элементарных нечетких высказываний, а T: U®[0, 1] — отображение истинности высказываний. Отрицанием (логическим) нечеткого высказывания A (обозначается ØA, читается как "не A") называется унарная логическая операция, результат которой является нечетким высказыванием, истинность ее есть: T (ØA) =1–T(A). (1.10) Конъюнкцией (логической) нечетких высказываний A и B (обозначается AÙB, читается как "A и B") называется бинарная логическая операция, результат которой является нечетким высказыванием, истинность которого: T(AÙB) = min{T(A), T(B)}. (1.11) Конъюнкцию нечетких высказываний также называют нечетким логическим "И";, нечеткой конъюнкцией или min-конъюнкцией и записывают в форме A AND B. Формулу (1.11) принимают основной для определения степени истинности конъюнкции. Для определения степени истинности конъюнкции нечетких высказываний могут быть использованы следующие альтернативные формулы. Алгебраическое произведение степеней истинности нечетких высказываний (обозначается A·B): T(AÙB) = T(A)×T(B). (1.12) Граничное произведение степеней истинности нечетких высказываний (обозначается A€B): T(AÙB) = max{T(A)+T(B) -1, 0}. (1.13) Драстическое произведение степеней истинности нечетких высказываний (обозначается ADB):
Дизъюнкцией (логической) нечетких высказываний A и B (обозначается A Ú B —читается "A или B") называется бинарная логическая операция, результат которой является нечетким высказыванием, истинность которого есть: T(A Ú B) = max{T(A), T(B)}. (1.15) Эту операцию также называют нечетким не исключающим логическим "ИЛИ", нечеткой дизъюнкцией или max-дизъюнкцией и иногда записывают также в форме A OR B. Формулу (1.15) считают основной для определения степени истинности дизъюнкции нечетких высказываний. Для определения степени истинности дизъюнкции нечетких высказываний могут быть использованы следующие альтернативные формулы. Алгебраическая сумма степеней истинности нечетких высказываний (обозначается A + B): T(A Ú B) = T(A)+T(B) -T(A)×T(B) (1.16) Алгебраическую сумму часто называют также вероятностной суммой. Граничная сумма степеней истинности нечетких высказываний (обозначается A Å B): T(A Ú B) = min{T(A)+T(B), 1} (1.17) Драстическая сумма степеней истинности нечетких высказываний (обозначается A Ñ B):
Замечание. В общем случае для определения истинности результатов нечеткой конъюнкции и нечеткой дизъюнкции могут использоваться и другие расчетные формулы, основанные на рассмотрении треугольных норм и конорм (произвольных функций 2-х переменных, удовлетворяющих ряду аксиом). Нечеткой импликацией, или просто импликацией нечетких высказываний A и B (записывается как: AÉB и читается — "из A следует B", "ЕСЛИA,ТО B "), называется бинарная логическая операция, результат которой является нечетким высказыванием, истинность которого определяется по одной из следующих формул. r Классическая нечеткая импликация Л. Заде: T(AÉB) = max{min{T(A), T(B)}, 1–T(A)}. r Классическая нечеткая импликация для случаяT(A)³T(B): T(AÉB) = max{T(ØA), T(B)}= max{1–T(A), T(B)}. Эту форму нечеткой импликации иногда называют нечеткой импликацией Гёделя. r Нечеткая импликация, предложенная Э. Мамдани: T(AÉ B) = min{T(A), T(B)}. Эту форму нечеткой импликации также называют нечеткой импликацией минимума корреляции. Заметим, что в случае T(A)³0.5 и T(B)³0.5 классическая нечеткая импликация превращается в нечеткую импликацию Мамдани. Кроме приведенных формул, существуют также варианты нечеткой импликации, предложенные Я.Лукасевичем, Дж.Гогеном, Н.Вади и др. Выбор того или иного варианта нечеткой импликации определяется с учетом характера решаемой прикладной задачи и простоты вычислений.
|