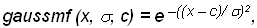Определение функций принадлежности

Для определения функций принадлежности нечет­ких множеств могут быть использованы пря­мые и косвенные методы.

При использовании прямых методов эксперт либо просто задает для каждого х Î Е значение µ_A (x), либо определяет функцию совместимости. Прямые методы задания функции принадлежности обычно ис­пользуются для измеримых понятий, таких как скорость, время, расстояние, температура и т.д., или когда выделяются полярные значения.

Во многих задачах при характеристике объекта можно выде­лить набор признаков и для каждого из них определить полярные значения, соответствующие значениям функции принадлежности, 0 или 1.

Например, в задаче определения характеристик и субхарактеристик качества программного обеспечения (согласно международному стандарту ISO 9126-1) можно выделить шкалы, приведенные в таблице 1.1.

Таблица 1.1. Шкалы в задаче оценки характеристик качества ПО

Для конкретного программного продукта A эксперт, исходя из приведенной шка­лы, задает µ_A (x)Î; [0; 1], формируя векторную функцию принад­лежности { µ_A (x₁), µ_A (x₂),… µ_A (x₉) }.

При прямых методах используются также групповые прямые методы, когда, например, группе экспертов предъявляют конкрет­ный программный продукт и каждый должен дать один из двух ответов: «это ПО надежное» или «это ПО не надежное», тогда количество утвердительных ответов, деленное на общее число экспертов, дает значение µ_{надежное} (ПО).

Косвенные методы определения значений функции принад­лежности используются в случаях, когда нет элементарных из­меримых свойств, через которые определяется нечеткое множество. Как правило, это методы попарных срав­нений. Если бы значения функций принадлежности были бы нам известны, например, µ_A(x_i) = ω_i, i = 1, 2,..., n, то попарные сравнения можно было бы представить матрицей отношений А= {a_ij}, где a_ij = ω_i / ω_j.

На практике эксперт формирует матрицу А, при этом предполагается, что диагональные элементы равны 1, а для элементов, симметричных относительно диагонали, a_ij =1/ a_ij, т.е. если один элемент оценивается в а раз сильнее чем другой, то этот по­следний должен быть в а раз сильнее, чем первый. В общем случае задача сводится к поиску вектора w, удовлетворяющего уравнению вида Aw = l_max\ w, где l_max  наибольшее собствен­ное значение матрицы А. Поскольку матрица А положительна по построению, решение данной задачи существует и является поло­жительным.

Можно отметить еще два подхода:

• использование относительных частот по данным экспе­римента в качестве значений функции принадлежности;

• использование типовых форм кривых для задания функций принадлежности с уточнением их параметров в соответствии с данными эксперимента.

Обычно используются следующие типовые формы функций принадлежности нечетких множеств: треугольная (trimf), трапецеидальная (trapmf), гауссова (gaussmf), двойная гауссова, обобщенная колоколообразная, сигмоидальная, двойная сигмоидальная, Z-функция, S-функция, Pi-функция.

Конкретный вид функций принадлежности определяется значениями параметров их аналитического представления, на­пример:

и т.д.